42- Determine as forças nos elementos e . Após a treliça ser secionada, utilize uma única equação de equilíbrio para o cálculo de cada força. Indique se esses elementos estão sob tração ou compressão.
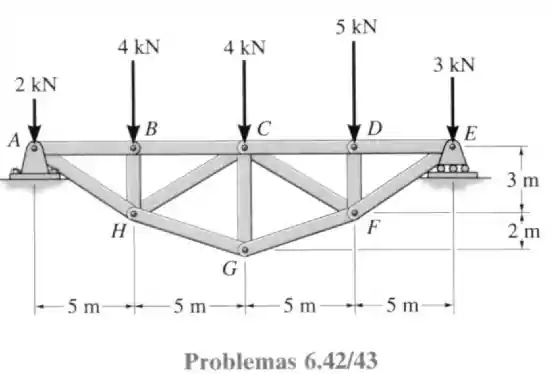
Passo 1
Antes de partir para o que a questão pede vamos calcular as reações nos apoios e .
A estrutura equivalente será:
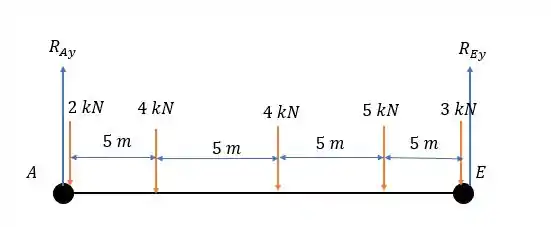
Fazendo a somatória das forças verticais temos:
E a somatória dos momentos em dá:
Logo:
Passo 2
Agora vamos cortar as barras e e analisar sua estrutura a esquerda desse corte.
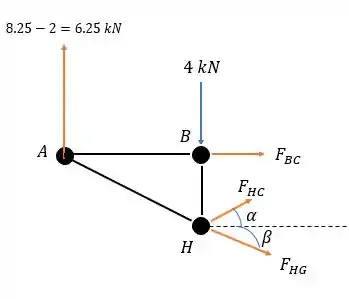
Onde pode ser calculador por:
E vale:
A proposta desse exercício é calcular uma força de cada vez sem precisar de uma outra equação para encontrar o valor de uma variável.
Passo 3
Como tem duas forças no ponto vamos resolver a somatória dos momentos em .
Força compressiva.
Passo 4
Agora vamos fazer a somatória dos momentos em pois também tem duas forças que vão para esse ponto.
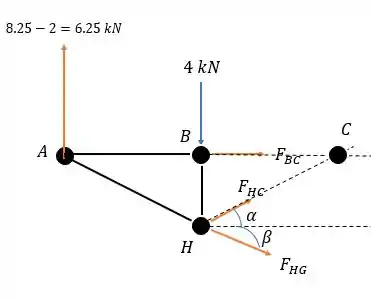
Passo 5
Agora basta encontrar o valor de para isso vamos fazer a somatória das forças verticais: