Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas Fundamentais - Ex. 18
Determine a força resultante que atua sobre o gancho.
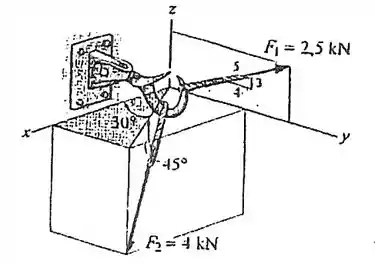
Passo 1
Vamos começar encontrando as componentes de cada força:
Força :
Essa força está no plano , então fica tranquilinho encontrar suas componentes pela relação do triângulo dado:
Em :
Em :
Assim, o vetor cartesiano de fica:
Passo 2
Vamos decompor agora a , nessa força já temos três componentes.
De início já podemos encontrar a direção , dado que a força faz com o plano :
Já, a projeção no plano é dada por:
E então decompor em e :
Temos em
E temos em :
E o vetor cartesiano de fica:
Perceba que coloquei a direção negativa de acordo com o sentido da força na imagem, fiquem atentos nisso.
Passo 3
Finalmente somamos as forças e para encontrar a força resultante: