Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 130
Se possui uma intensidade de , determine a intensidade de suas componentes projetadas que atuam ao longo do eixo e do cabo .
Passo 1
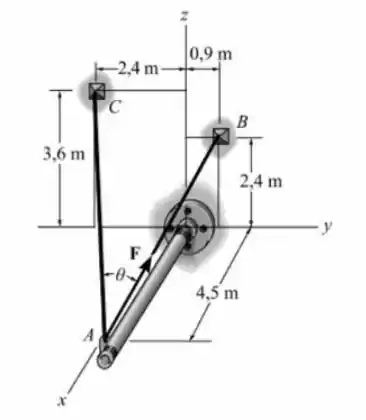
Show de bolinhas galera, tudo beleza com vocês?! Saca só, nesse exercício aqui, o enunciado nos deu uma força atuando em um ponto através de uma linha de ação como na figura a seguir:
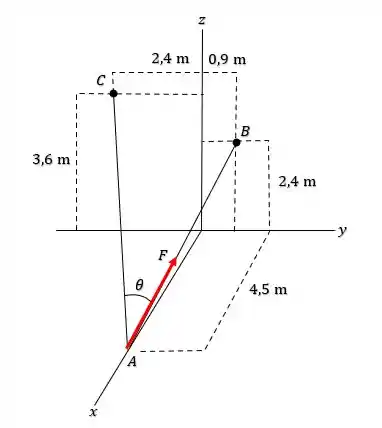
Com base nesses dados, o enunciado nos pede pra calcular o valor da projeção da força sobre a linha de ação e sobre o eixo .
Mas calma lá meu patrão, vamos devagarinho. A gente que para projetar um vetor sobre um vetor , utilizamos a fórmula:
Onde representa o produto interno entre e , enquanto que representa o módulo do vetor . Então pra gente projetar a força em alguma reta precisamos saber a expressão vetorial da nossa força e também da nossa reta.
Passo 2
Bom galaerinha, primeiro vamos encontrar a equação vetorial da força que iremos trabalhar, pra isso vamos lembrar que podemos expressar a equação vetorial da força como:
Onde é o vetor unitário da direção de . Sabemos que a direção da força é no sentido do ponto para o ponto , onde esse pontos são expressos como:
De modo que o segmento é orientado como:
Então isso quer dizer que o vetor normal dessa direção, , será dado como:
Ou então:
Iradoso, e como a força possui um módulo de , quer dizer que sua equação vetorial vai ser dada como:
Então de cara já matamos também qual é a projeção da força no eixo , afinal essa componente é quem acomponha o vetor unitário , então a intensidade de será:
Passo 3
Agora pra gente projetar a força na linha , precisamos primeiro encontrar o vetor diretor desse segmento, e pra isso vamos precisamos dos pontos e , que são dados como:
Então o vetor diretor será:
Ou então:
E seu módulo é:
Então vamos ter que a projeção da força sobre esse vetor será dada como:
Tal que o produto interno entre a força e o vetor será:
Sendo assim, vamos obter que a projeção de sobre será:
Isso quer dizer que a intensidade dessa força vai ser:
Prontinha galerinha, é isto!!
