Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 4.Problemas Fundamentais - Ex. 42
Determine a força resultante e especifique onde ela atua na viga, medindo a partir do ponto .
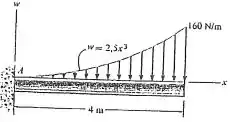
Passo 1
A fim de determinar a força resultante, a sua intensidade equivale à soma de todas as forças que estão atuando na carga distribuída. Por esse fato e por ser fornecido, é possível determinar a resultante através da seguinte integração:
E a sua posição de atuação em relação ao ponto pode ser determinada através do centroide da área abaixo do carregamento distribuído que é dado por:
Passo 2
Sendo assim, dadas as informações e a equação da força resultante, pode-se calcular seu valor:
Logo,
Passo 3
Agora, utilizando a equação do centroide da área do carregamento consegue-se obter a posição de atuação da força resultante já que ela tem uma linha de ação que passa pelo centroide, tal que:
Portanto,
Resposta
à direita de