Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 6.Problemas fundamentais - Ex. 4
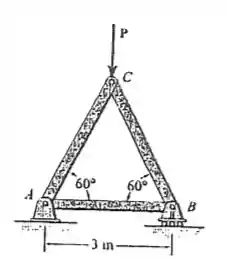
Determine a maior carga que pode ser aplicado na treliça de modo que nenhum dos membros esteja sujeito a uma força excedendo em tração ou em compressão.
Passo 1
E aí meus cheiros, prontos pra mais uma questão bacaninha?
Pois bem, queremos determinar o maior valor de que pode ser aplicado na nossa treliça de tal forma que nenhum dos nossos membros esteja sujeito a uma força de em tração ou em compressão. Sendo assim, bora primeiro esquematizar um diagrama de corpo livre pra facilitar nossa vida aqui com esse problema, podemos representá-lo como
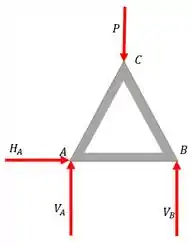
Porque não temos outra força nessa direção.
Uma coisa que é importante a gente prestar atenção nesse problema é a simetria da nossa treliça. Então o que a gente achar para , vale para .
Isso quer dizer também que por causa da simetria :
Sendo assim, vamos fazer a análise nos nós pra ir logo encontrando o que desejamos sem ter muito trabalho.
Passo 2
Começando pelo nó .
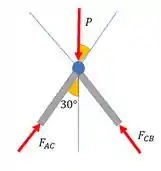
Pela simetria do problema vamos ter . Para projetar essas forças em , multiplicamos elas por cosseno de , porque esse ângulo está colado em . Então teremos
Vemos que é compressão pela figura, a setinha está entrando na peça, ok?
Pois bem, como o valor máximo para a compressão é podemos fazer
Passo 3
Precisamos, agora, encontrar uma expressão pra tração de tal forma que consigamos comparar os valores de para pegar o maior como a questão solicita. E agora José? Calma, calma, vamos fazer a mesma avaliação anterior só que agora para o Nó de tal forma que encontraremos
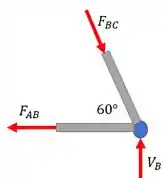
Vimos quando vale no passo anterior:
Achamos uma expressão para tração, mas ela vai ser a única? Sim, devido a simetria do nosso problema (eu disse que ela era um fator importante). Para a tração temos que o valor máximo é então teremos
Pronto, agora basta decidir qual dos dois valores de é o menor. Por que? Porque aí a gente garante que ambos os critérios serão atendidos. Ou seja, não vai ser maior que o permitido para tração e para compressão. Logo: