Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 4.Problemas - Ex. 84
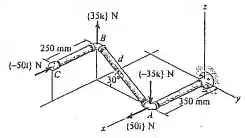
Determine a distância entre e tal que o momento de binário resultante tenha uma intensidade de .
Passo 1
Fala, querido!
A questão pede a distância para que a intensidade do binário resultante seja . Para acharmos isso, precisamos escrever o binário resultante em termos de .
A fórmula para um binário de duas forças antiparalelas separadas por um vetor é
Assim, temos que calcular cada um dos binários e somá-los vetorialmente.
Bora montar a expressão do binário resultante e igualar ao valor que ele deu.
Passo 2
pode ser escolhido de algumas formas.
Tudo bem a forma que escolher, desde que ele esteja entre a linha de ação das duas forças. E esteja apontando para a linha da força que vai usar nas continhas. Vamos escolher assim: vai ser o vetor que sai do ponto de aplicação de uma força até ponto de aplicação da outra.
Para gente . O vetor que sai do ponto de aplicação da outra força do binário e vai até o ponto de aplicação dessa força no sentido positivo vai ser a diferença entre as coordenadas desses pontos. O ponto e é:
Nosso vetor fica:
Já para o outro binário, vamos escolher . O ponto de aplicação dessa força é e da outra força do binário é . Então nosso pode ser:
Passo 3
Calculando os produtos vetoriais:
Obs: Aqui cê pode calcular o produto vetorial fazendo o determinante também. Dá o mesmo valor. Aí fica seu critério, tá?
Portanto,
Assim, a intensidade do binário resultante será o módulo desse vetor:
Por causa daquela identidade , ficamos com
Desta forma,
Passo 4
Substituindo , e , obtemos
Portanto, .