Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 4.Problemas Fundamentais - Ex. 41
Determine a força resultante e especifique onde ela atua na viga, medindo a partir do ponto .
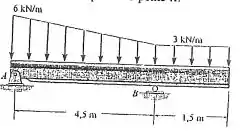
Passo 1
A fim de determinar a força resultante, a sua intensidade equivale à soma de todas as forças que estão atuando na carga distribuída. Por esse fato, a resultante que seria definida pela integração entre uma força por unidade de comprimento e um elemento de comprimento, ela pode ser determinada pela área abaixo da curva da carga distribuída, ou seja:
E a sua posição de atuação em relação ao ponto pode ser determinada através do princípio dos momentos, já que são relacionadas as forças envolvidas e a distância delas até o ponto de referência para os momentos ocorrerem.
Passo 2
Como uma parte da força distribuída deste caso é trapezoidal, esta pode ser dividida em duas áreas mais simples tal como um retângulo (que pode ser mesclada com a outra parte já retangular) e um triângulo. Então, a força resultante será dada pela soma dessas duas áreas:
Logo,
Passo 3
Agora, para saber a distância do ponto de atuação da força resultante até o ponto deve ser feito o somatório de momentos em relação a esse ponto, tal que a força distribuída foi dividida e representada por uma área triangular e uma retangular.
Lembrando que a distância para calcular o momento gerado por uma força distribuída é dada pela posição do centroide da área até o ponto de referência, deve-se lembrar também que a posição do centroide de um triângulo é calculada como:
E do centroide de um retângulo é:
Passo 4
Logo, aplicando o princípio dos momentos em relação ao ponto , admitindo que o momento é positivo no sentido horário, tem-se que:
Resposta
à direita de