30- Determine as forças nos elementos e para a treliça da ponte e indique se eles estão sob tração ou compressão.
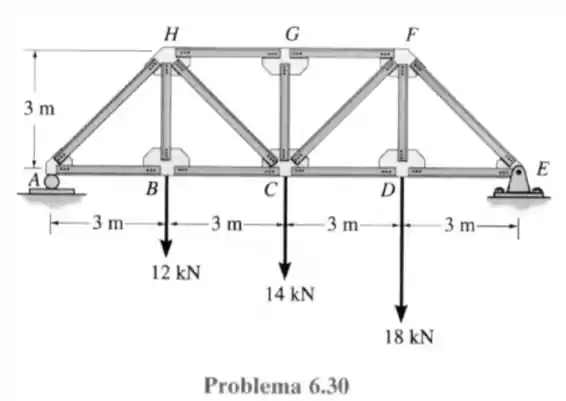
Passo 1
Primeiramente vamos calcular a força de reação nos apoios e sabendo que não há forças ativas horizontais, portanto não existe reação horizontal nos apoios.
Isso nos dá o seguinte sistema de forças.
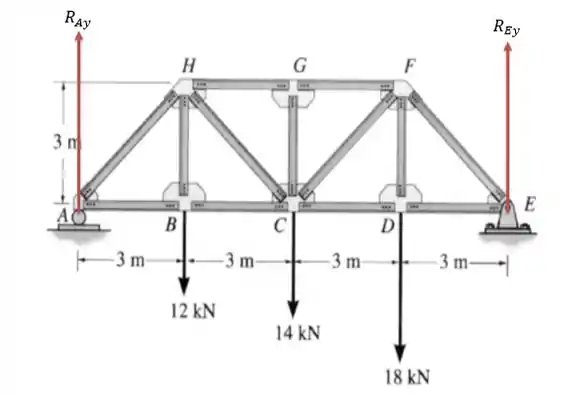
Fazendo a somatória das forças verticais nós iremos ter:
E se fizermos a somatória dos momentos em nós vamos conseguir:
Logo:
Passo 2
Agora note que conseguimos cortar as barras , e barras onde queremos dizer suas respectivas forças, então vamos cortar essas barras e expor as forças saindo de seus nós.
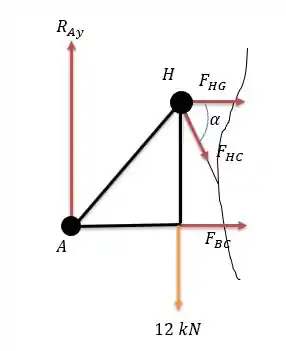
Onde será calculado por:
E já podemos calcular o valor de fazendo a somatória das forças verticais. Uma das graças do método dos nós é que a partir de agora tratamos as forças nas barras cortadas como forças ativas. Então assim sendo:
Passo 3
Agora vamos precisar fazer momento para calcular as outras duas forças restantes.
O primeiro será , considerando o sentido horário como positivo e qualquer força que atue paralela ao eixo a qual ela está não gera momento, o que nos dá:
Agora a somatória dos momentos em .
Onde obrigatoriamente temos que fazer os momentos das projeções da força.