Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 2.Problemas - Ex. 66

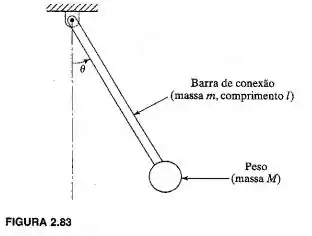
Determine a frequência natural do pêndulo mostrado na Figura 2.83, quando a massa da barra conectora não é desprezível em comparação com a massa do peso do pêndulo.

Passo 1

Vamos calcular a energia cinética do sistema:

T = T h a s + T p e n

T = 1 2 J h a s θ ˙ 2 + 1 2 J p e n θ ˙ 2

Onde os índices h a s e p e n indicam a haste e o pêndulo com relação ao pivô, respectivamente.

Substituindo os momentos de inércia mássicos, temos que:

T = 1 2 1 3 m l 2 θ ˙ 2 + 1 2 M l 2 θ ˙ 2

Podemos calcular também a energia potencial do sistema:

U = U h a s + U p e n

U = 1 2 m g l 1 - cos ⁡ θ + M g l 1 - cos ⁡ θ

Temos que a equação de movimento para o sistema é dada por:

d d t T + U = 0

d d t 1 2 1 3 m l 2 θ ˙ 2 + 1 2 M l 2 θ ˙ 2 + 1 2 m g l 1 - cos ⁡ θ + M g l 1 - cos ⁡ θ = 0

Resolvendo, temos que:

M + m 3 l 2 θ ¨ + M + m 2 g l sen ⁡ θ = 0

θ ¨ + M + m 2 M + m 3 g l θ = 0

Comparando com a equação de movimento do sistema, onde:

θ ¨ + ω n 2 θ = 0

Temos que:

ω n = M + m 2 M + m 3 g l

Resposta

ω n = M + m 2 M + m 3 g l

Ver Outros Exercícios desse livro