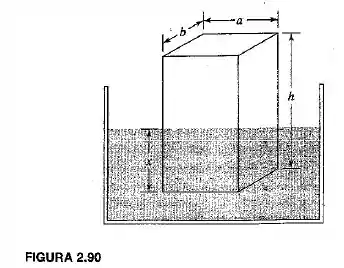
Um prisma retangular de madeira com densidade , altura e seção transversal é inicialmente comprimido dentro de uma cuba de óleo e vibra livremente no sentido vertical (Figura ). Use o método de Rayleigh para determinar a frequência natural de vibração do prisma. Considere que a densidade do óleo é . Se o prisma retangular for substituído por um cilindro circular uniforme de raio , altura e densidade , ocorrerá alguma alteração na frequência natural?

Queremos a frequência natural de vibração do prisma pelo método de Rayleigh.

Vamos calcular a força de restauração do óleo quando o prisma é deslocado do equilíbrio:

Temos que:

Logo:

Temos que a equação de movimento para o sistema é da seguinte forma:

Substituindo por , temos que: