Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 6.Problemas - Ex. 46

Determine as frequências naturais e formas modais do sistema mostrado na Figura 6.6(a) quando k 1 = k ,   k 2 = 2 k ,   k 3 = 3 k ,   m 1 = m ,   m 2 = 2 m ,   m 3 = 3 m . Faça um gráfico das formas modais.

Passo 1

Olá pessoal, tudo bem com vocês? Vamos agr pra mais uma questão desse assunto, quem tem matrizes até demais mas a gente dá conta kkk

Bom, lá do problema 6.19, nós já conseguimos as equações de movimento, que na forma matricial e aplicando para os dados dessa questão, são as seguintes:

m 1           0           0 0           m 2           0 0           0           m 3 x 1 ¨ x 2 x 3 ¨ ¨ + k 1 + k 2         - k 2                 0 - k 2           k 2 + k 3         - k 3 0                         - k 3                         k 3 x 1 x 2 x 3 = 0 0 0

Por definição para um movimento harmônico, o sistema fica assim:

- ω 2 m 1 + k 1 + k 2             - k 2                     0 - k 2       - ω 2 m 2 +   k 2 + k 3         - k 3 0                                 - k 3               - ω 2 m 3 + k 3 x 1 x 2 x 3 = 0 0 0

Consequentemente, as equações de frequência (com k 1 = k ,   k 2 = 2 k ,   k 3 = 3 k ,   m 1 = m ,   m 2 = 2 m ,   m 3 = 3 m ) são:

- ω 2 m + 3 k                     - 2 k                               0 - 2 k                 - 2 ω 2 m + 5 k               - 3 k 0                                 - 3 k               - 3 ω 2 m + 3 k = 0 0 0

Agora tirando da forma matricial, temos que:

- ω 2 m + 3 k - 2 ω 2 m + 5 k - 3 ω 2 m + 3 k - 9 k 2 + 2 k - 2 k ( - 3 ω 2 m + 3 k ) = 0

De onde nós tiramos que:

- 2 α 3 - 13 α 2 + 19 α - 2 = 0

Com α = ω 2 m k .

Passo 2

Dada essa última equação, nós podemos extrair as seguintes raízes:

α 1 = 0,113992 → ω 1 = 0,337627 k / m

α 2 = 2,00002 → ω 2 = 1,414221 k / m

α 3 = 4,38600 → ω 3 = 2,094278 k / m

Colocando na forma modal de modo j t h , a equação de movimento harmônico nos dá que:

x 2 j x 1 j = - ω j 2 m 1 + k 1 + k 2 k 2 = - ω j 2 m + 3 k 2 k

x 3 j x 2 j = k 3 - ω j 2 m 3 + k 3 = 3 k - 3 ω j 2 m + 3 k

x 3 j x 1 j = x 3 j x 2 j ∙ x 2 j x 1 j = 3 ( - ω j 2 m + 3 k ) 2 ( - 3 ω j 2 m + 3 k )

Passo 3

Para tanto, nós temos para as formas modais, a seguinte relação:

x j → = x 1 j x 2 j x 3 j = x i j 1 - ω j 2 m + 3 k 2 k 3 ( - ω j 2 m + 3 k ) 2 ( - 3 ω j 2 m + 3 k )

Ou seja:

x ( 1 ) → = x 1 ( 1 ) 1 1,443004 1,628659 ,       x ( 2 ) → = x 1 ( 2 ) 1 0,49999 - 0,49998 ,         x ( 3 ) → = x 1 ( 3 ) 1 - 0,693 0,204666

E finalmente, temos nas ilustrações a seguir, os gráficos pedidos na questão, representando as formas modais:

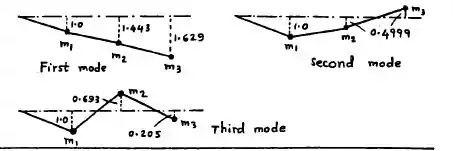
Resposta

x ( 1 ) → = x 1 ( 1 ) 1 1,443004 1,628659 ,       x ( 2 ) → = x 1 ( 2 ) 1 0,49999 - 0,49998 ,         x ( 3 ) → = x 1 ( 3 ) 1 - 0,693 0,204666

Ver Outros Exercícios desse livro