Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 6.Problemas - Ex. 48

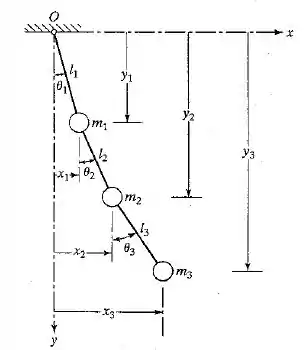
Determine as frequências naturais do sistema mostrado na Figura 6.10 com l 1 = 20 c m ,   l 2 = 30 c m ,   l 3 = 40   c m ,   m 1 = 1 k g ,   m 2 = 2 k g ,   m 3 = 3 k g .

Passo 1

Falaaa meus amigos! Como vocês estão? Vamos pra mais uma questãozinha desse assunto?

Bom, para esses dados do enunciado, o problema anterior, 6.37, já nos fornece o esquema das equações de movimento, que com as devidas modificações vão ficar:

6 0,04         5 0,06         3 0,08 5 0,06         5 0,09           3 0,12 3 0,08         3 0,12           3 ( 0,16 ) θ 1 ¨ θ 2 θ 3 ¨ ¨ + 6 ( 9,81 ) ( 0,2 )         0       0 0         5 9,81 ) ( 0,3           0 0         0           3 ( 9,81 ) ( 0,4 ) θ 1 θ 2 θ 3 = 0 0 0

Pela definição de movimento harmônico, esse sistema se torna o seguinte:

- ω 2 0,24           0,30         0,24 0,30         0,45           0,36 0,24         0,36           0,48 H 1 ^ H 2 ^ H 3 ^ + 11,772         0       0 0         14,715           0 0         0           11,772 H 1 ^ H 2 ^ H 3 ^ = 0 0 0

Passo 2

Esse sistema nos dá a seguinte equação de frequência:

ω 2 0,24 - 11,772           ω 2 0,30         ω 2 0,24 ω 2 0,30         ω 2 0,45 - 14,715           ω 2 0,36 ω 2 0,24         ω 2 0,36           ω 2 0,48 - 11,7772 = 0

Ou seja, tirando da forma matricial:

ω 2 0,24   ω 2 0,45 - 14,715   ω 2 0,48 - 11,7772 - 0,36 2 ω 4 - 0,3 ω 2 0,3 ω 2   ω 2 0,48 - 11,7772 - 0,24 0,36 ω 4 + 0,24 ω 2 0,30 0,36 ω 4 + 54132,806 ω 2 - 590047,6 = 0

As raízes desta mega expressão vão ser:

ω 1 2 = 12,6335 → ω 1 = 3,554364   r a d / s

ω 2 2 = 94,6116 → ω 2 = 9,726849   r a d / s

ω 3 2 = 4 93,619 → ω 3 = 22,217538   r a d / s

Resposta

ω 1 = 3,554364   r a d / s

ω 2 = 9,726849   r a d / s

ω 3 = 22,217538   r a d / s

Ver Outros Exercícios desse livro