Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 7

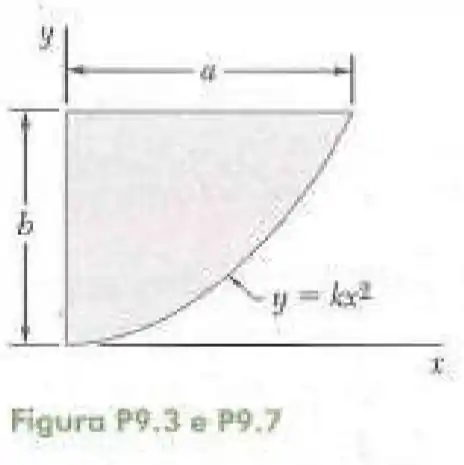
7- Determine por integração direta o momento de inércia da superfície sombreada em relação ao eixo x .

Passo 1

Para calcular a inércia no eixo x precisamos traçar várias linhas horizontais com o objetivo de encontrar o elemento de área d A , fazendo com que tenhamos a seguinte fórmula para essa inércia.

I x = ∫ y 2   d A

Onde agora precisaremos da equação de x em relação a y da parábola.

Pelo exercício 3 encontramos que a equação dessa parábola vale:

y = b a 2   x 2

x = a 2 y b

Passo 2

Agora vamos pegar linhas horizontais da parábola:

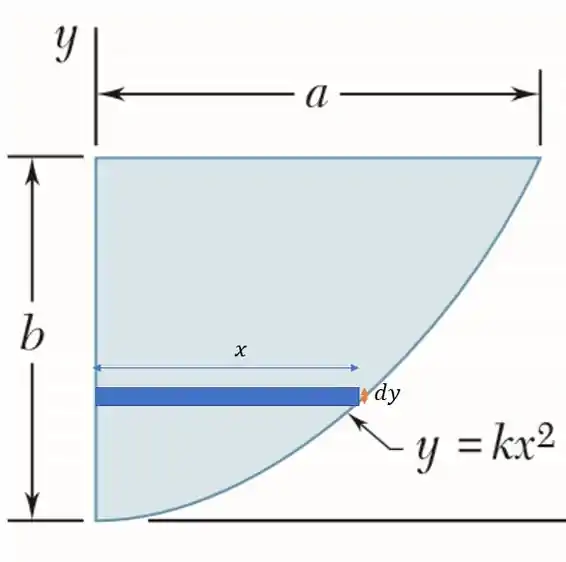
Dessa forma:

d A = x   d y

Passo 3

Deixando nossa integral com a seguinte cara:

I x = ∫ y 2   d A

Como y varia de 0 até b nós temos:

I x = ∫ 0 b y 2   x   d y

Onde x = a 2 y b , o que nos dá:

I x = ∫ 0 b y 2   a 2 y b d y

O que nos dá:

I x = ∫ 0 b y 2 a b 1 2 y 1 2   d y

I x = a b 1 2   ∫ 0 b y 5 2   d y

I x = a b 1 2 y 7 2 7 2 0 b

I x = 2 a b 7 2 7 b 1 2 = 2 a b 3 7

Resposta

I x = 2 a b 3 7

Ver Outros Exercícios desse livro