Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 71
71- Usando o método da Seção , resolva o Problema .
Passo 1
Viga do Problema .
Problema.
Para a viga e o carregamento mostrados na figura, trace os diagramas de esforço cortante e do momento fletor determine os valores absolutos máximos do esforço cortante e do momento fletor.
Sabendo que o carregamento de exerce uma força resultante de :
Há uma distância de do apoio de primeiro gênero em . Nos dando a seguinte viga equivalente.
Pela somatória das forças horizontai temos que:
E pela somatória das forças verticais vemos que:
E fazendo a somatória dos momentos em .
Dessa forma:
Passo 2
Vamos encontrar por seção as cortantes e momentos equivalente.
Começando pela seção indo de :
Nessa seção vemos que pela soma das forças verticais que:
E pela somatória dos momentos:
Onde que para , temos
Aproveitando a força resultante e o momento resultante da seção anterior nós podemos avançar para o intervalo de :
Pela somatória das forças verticais vemos que a cortante nessa seção vale:
E o momento valerá então:
Onde vale e , nos dando:
Onde que para teremos um momento de:
Agora para o intervalo de :
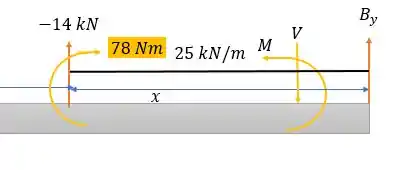
Pela somatória das forças verticais vemos que:
Onde que para temos um cortante igual a:
Cortante essa que se anulará com a reação em (isso é uma prova que fizemos tudo certo até aqui).
Agora para os momentos temos:
Onde que para vemos que:
O que prova que está tudo certo. Com isso achamos o maior valor de cortante absoluto igual a e o maior de momento absoluto igual a .
Passo 3
Os gráficos de diagrama cortante e de momento fletor são:
Diagrama da cortante.
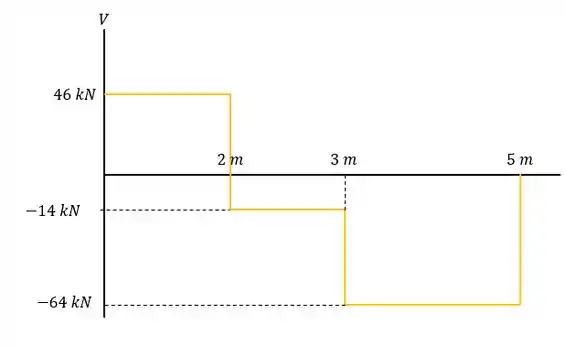
Diagrama do momento fletor.
