Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 4

4- Determine por integração direta o momento de inércia da superfície sombreada em relação ao eixo y .

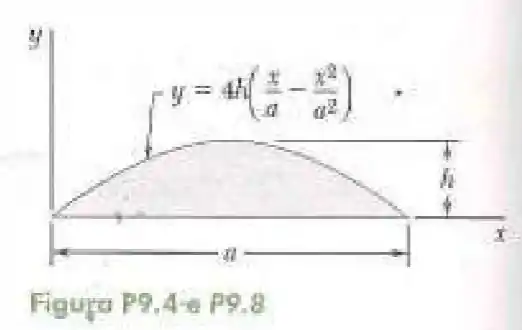
Passo 1

Sabendo que a integração em y se faz da seguinte forma:

I y = ∫ x 2   d A

E que traçando linhas verticais nós chegamos na seguinte fórmula de elemento de área.

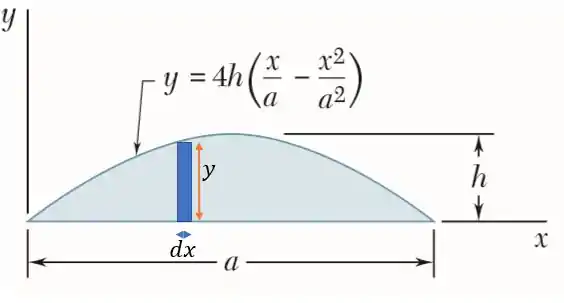
Onde d A pela imagem vale:

d A = y   d x

Passo 2

Isso deixa nossa inércia da seguinte forma:

I y = ∫ x 2   y   d x

Onde y = 4 h x a - x 2 a 2 e x varia de 0 até a .

Logo:

I y = ∫ 0 a x 2   4 h x a - x 2 a 2   d x

Dessa forma:

I y = 4 h ∫ 0 a x 3 a - x 4 a 2 d x  

Fazendo a integral temos:

I y = 4 h x 4 4 a - x 5 5 a 2 0 a

Aplicando o intervalo:

I y = 4 h a 4 4 a - a 5 5 a 2 = 4 h a 3 4 - a 3 5 = 4 h a 3 20 = h a 3 5

Resposta

I y = h a 3 5

Ver Outros Exercícios desse livro