Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 5

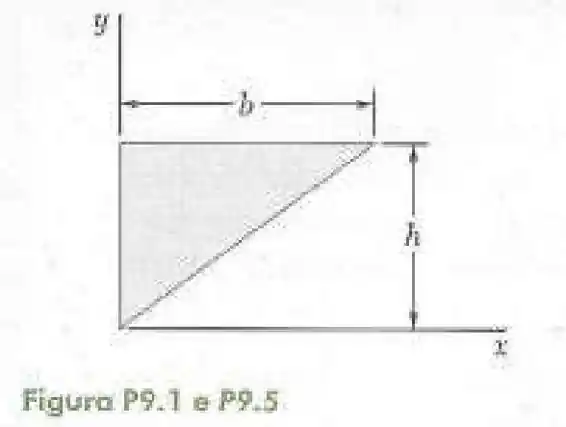
5- Determine por integração direta o momento de inércia da superfície sombreada em relação ao eixo x .

Passo 1

Para fazer a integral em relação ao eixo x nós precisamos fazer:

I x = ∫ y 2   d A

Onde agora ao invés de desenharmos linhas verticais para encontrarmos o elemento de área d A nós precisamos desenhar linhas horizontais. De formas que agora temos:

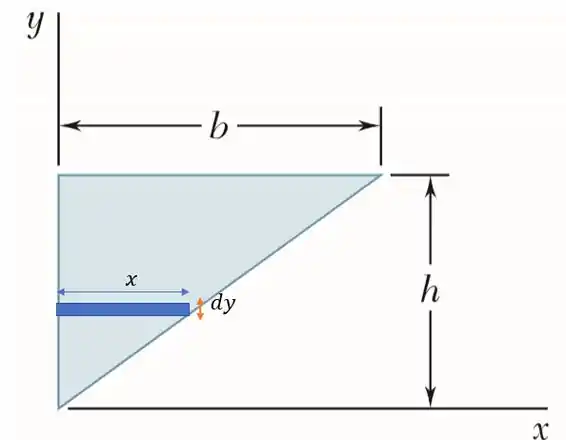
Onde a área dessa linha valerá:

d A = x d y

Passo 2

Um passo importante é sabermos a equação da reta que correlaciona x com y e como ela sai do ponto ( 0,0 ) podemos dizer que ela é da cara:

y = m x

Como o ponto de limite é ( b , h ) então m valerá:

h = m b

m = h b

Logo:

y = h x b

Ou:

x = b y h

Passo 3

Como y varia de 0 até h nós teremos a seguinte integral.

I x = ∫ 0 h y 2   x   d y

Onde x = b y h , deixando nossa integral da seguinte forma:

I x = ∫ 0 h y 2 × b y h   d y

I x = ∫ 0 h b h   y 3   d y

Então:

I x = b h y 4 4 0 h = b h 4 4 h = b h 3 4

Resposta

I x = b h 3 4

Ver Outros Exercícios desse livro