Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 3
3- Determine por integração direta o momento de inércia da superfície sombreada em relação ao eixo .
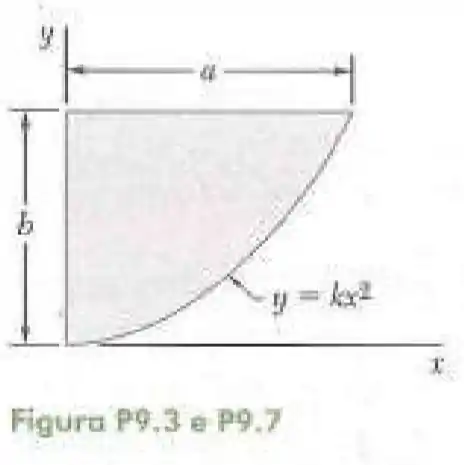
Passo 1
Para calcularmos o momento em relação ao eixo nós devemos fazer a seguinte integral
Pois a idéia de fazermos várias linhas verticais de largura e que estão longe da origem a uma distância . Mas antes de fazermos essa integral da função precisamos encontrar a constante .
Onde a parábola começa no ponto e termina no ponto , substituindo esse último ponto nós temos:
Logo:
Passo 2
Agora falta nós conseguimos dizer por meio dessa função o que significa .E para isso vamos ver quanto vale a área de uma simples linha vertical nessa superfície.
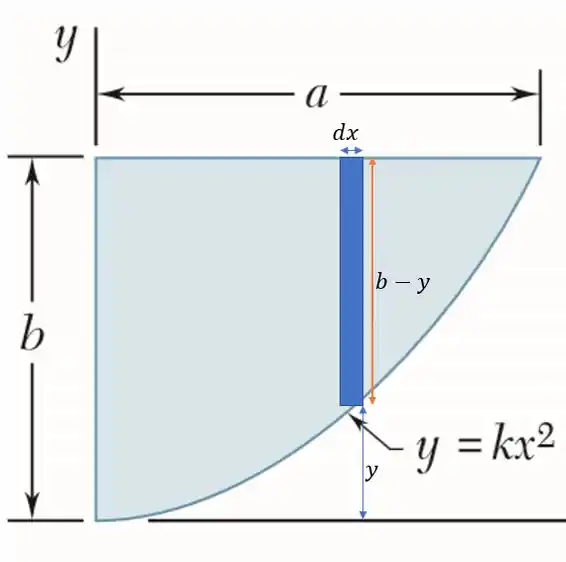
Isso é, não importa a linha vertical que formos pegar ela sempre terá altura igual a , pois está limitado entre a reta e da parábola. E terá largura de , nos dando então um elemento de área igual a:
O raciocínio é idêntico a quando calculamos o centro de massa ou de área. Pois nele precisamos calcular o momento em relação a um dos eixos.
Passo 3
Dessa forma a integral da inércia será igual a:
Pois nós encontramos e vale
E varia de até . Logo nossa integral fica:
Fazendo a integral:
Aplicando o intervalo: