Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 4

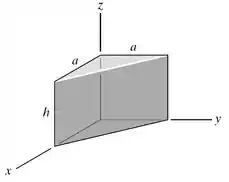
Determine por integração direta o produto de inércia I y z para o prisma homogêneo. A densidade do material é ρ . Expresse o resultado em termos da massa total m do prisma.

Passo 1

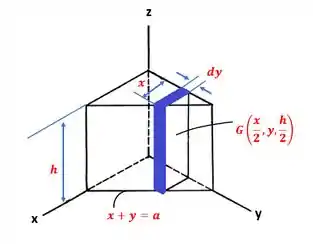
Nota-se que a massa infinitesimal do prisma homogêneo d m , é tal que pode ser escrita como:

d m = ρ d V = ρ h x d y = ρ h a - y d y

A massa m , será:

m = ∫ m d m = ρ h ∫ 0 a ( a - y ) d y = ρ a 2 h 2

Passo 2

Fazendo uso do teorema dos eixos paralelos entre os eixos y,z e os eixos y’ e z’ que passam pelo centro de gravidade do prisma homogêneo , temos que o momento de inércia para o elemento diferencial d I y z será:

d I y z = d I y ' z ' + d m y G z G = 0 + ( ρ h x d y ) ( y ) h 2

d I y z = ρ h 2 2 x y d y = ρ h 2 2 a y + y 2 d y

Passo 3

O momento de inércia I y z é obtido integrando-se   d I y z , de modo que:

I y z = ρ h 2 2 ∫ 0 a a y + y 2 d y = ρ a 3 h 2 12 = 1 6 ρ a 2 h 2 ( a h )

Portanto:

I y z = m 6 a h

Resposta

De acordo com os passos 1,2 e 3 o produto de inércia I y z para o prisma homogêneo expresso em termos da massa total m , será:

I y z = m 6 a h

Ver Outros Exercícios desse livro