Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 3

Determine os momentos de inércia I x e I y do paroboloide de revolução . A massa do paraboloide é m .

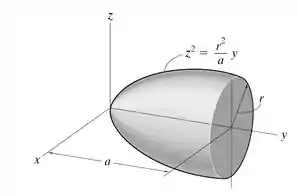
Passo 1

Nota-se que a massa infinitesimal do paraboloide d m , é tal que pode ser escrita como:

d m = ρ π z 2 d y = ρ π r 2 a y d y

A massa m , será:

m = ρ π ∫ 0 a r 2 a y d y = ρ π r 2 2 a

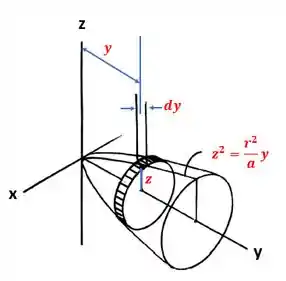
Passo 2

O momento de inércia I y será :

I y = ∫ m 1 2 d m   z 2 = 1 2 ρ π ∫ 0 a z 4 d y = 1 2 ρ π r 4 a 2 ∫ 0 a y 2 d y = ρ π r 4 6 a  

Portanto, temos que:

I y = 1 3 m r 2

Passo 3

O momento de inércia I x será :

I x = ∫ m 1 4   d m   z 2 + d m   y 2 = 1 4 ∫ 0 a z 4 d y + ρ π ∫ 0 a z 2 y 2 d y

I x = 1 4 ρ π r 4 a 2 ∫ 0 a y 2 d y + ρ π r 2 a ∫ 0 a y 3 d y = ρ π r 4 12 a + ρ π r 2 4 a 3  

Portanto, temos que :

I x = 1 6 m r 2 + 1 6 m a 2 =   m 6 r 2 + a 2

Resposta

De acordo com os passos 1,2 e 3 os moementos de inércia I x e I y do paroboloide de revolução são respectivamente:

I y = 1 3 m r 2

I x =   m 6 r 2 + a 2

Ver Outros Exercícios desse livro