23- Determine a intensidade e a direção da resultante das três forças, encontrando primeiro a resultante e depois compondo
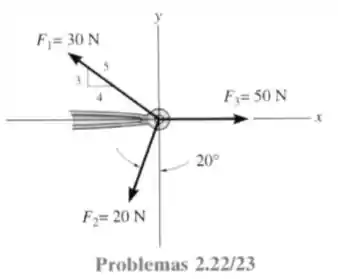
Passo 1
Decompondo as forças e nos eixos e temos:
Somando as duas forças temos:
Passo 2
Agora precisamos compor com a força que decomposta nos eixos valerá:
Somando todas as forças temos:
Esse vetor é aproximadamente igual a:
Aí é o mesmo procedimento da questão anterior.
Passo 3
Fazendo o módulo da força temos:
E a direção se dará:
Ou no sentido horário.