3- Determine a intensidade da força resultante e sua direção, medida no sentido anti-horário, a partir do eixo positivo.
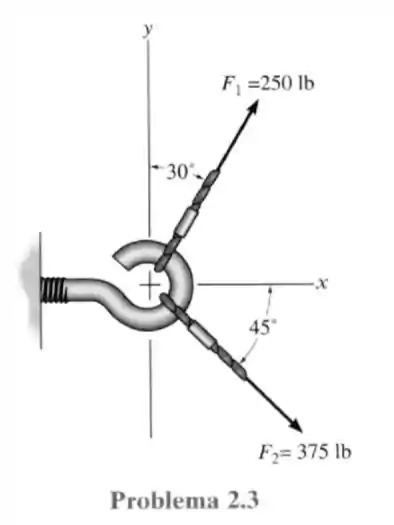
Passo 1
Decompondo a força temos:
Agora decompondo temos:
Uma vez que aponta para baixo, logo a componente vale zero.
Passo 2
Somando as duas forças agora temos:
Como a coordenada é negativa e é positiva logo a força está no quarto quadrante.
Passo 3
O módulo desse vetor vale:
Agora calculando o sentido:
Aplicando o arcotangente.
Como queremos o ângulo que sai do eixo e gire no sentido anti-horário tooooodo o percurso até chegar no ângulo em questão em temos que somar uma volta inteira para encontrar o valor positivo, logo: