Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 2.3 - Ex. 4
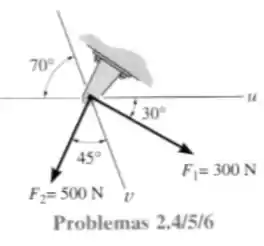
4- Determine a intensidade da força resultante e sua direção, medida no sentido anti-horário, a partir do eixo positivo.
Passo 1
Como as questões e se tratam da decomposição das forças no eixo e (que são eixos próprios dessa espécie de mancal não da para dizer o que exatamente isso é) então vamos fazer a lei dos cossenos para encontrar a força resultante desse sistema de forças.
Passo 2
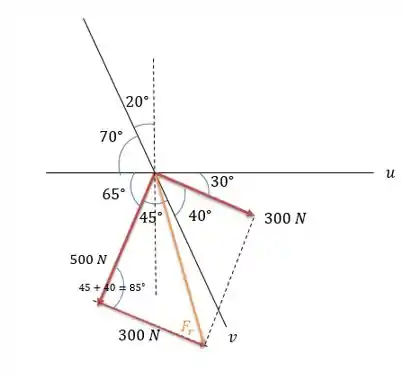
Dessa forma a força resultante será igual a:
Passo 3
Vamos arrumar um pouco o desenho para que conseguir calcular o ângulo no sentido anti-horário.
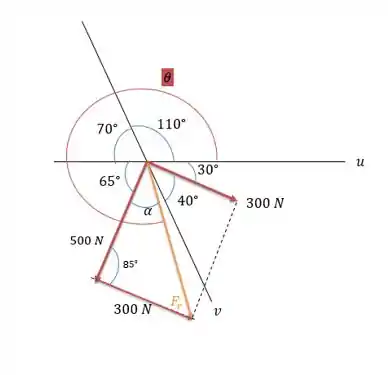
Começando a partir do sentido horário temos o ângulo complementar a que é o que falta para chegar a , isso é , o próprio , depois que vem da soma com o ângulo de para dar e um ângulo onde será possível encontrar por lei dos senos.
Note que não é pois esse ângulo é o ângulo que a força de faz com que eixo . O ângulo é só o ângulo formado pelo triângulo de forças.
Com o valor de que calculamos no passo anterior temos:
Fazendo o arco seno temos:
Logo o ângulo que tem com o eixo que tem sentido positivo indo para leste será de: