Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 126
Determine a localização do centroide para a forma estrutural. Despreze a espessura do membro.
Passo 1
O problema pede que encontremos o centroide no eixo , para isso vamos usar a formula do centroide:
Note que eu coloquei ao invés de , isso porque ao invés da área iremos usar o comprimento, já que é uma barra fina.
Passo 2
Então, primeiro vamos começar fazendo uma tabela com algumas informações para usar nas formulas do centroide:
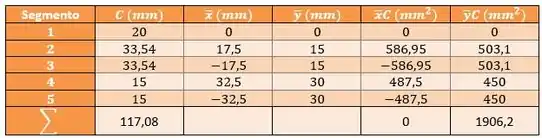
E a gente pode encontrar todos os centroides da figura no final do livro.
Passo 3
Então agora usar a formula do primeiro passo, com as informações do passo anterior para calcular o centroide:
Resposta
Exercícios de Livros Relacionados
Localize o centro de massa z - do sólido formado escavando-se um hemisfério na base do cilindro com um cone no topo. O cone e o cilindro são feitos de materiais com densidades de 7,80M g / m 3 e 2,70M
Um foguete de brinquedo consiste em um topo cônico sólido, ρ t = 600k g / m 3 , um cilindro oco, ρ c = 400k g / m 3 e uma vara com uma seção transversal circular, ρ v = 300k g / m 3 . Determine o comp
Localize o centro de massa z - do sólido consistindo em um núcleo central cilíndrico A , com densidade de 7,90M g / m 3 , uma parte externa cilíndrica B e um cone C no topo, cada um desses dois último
Um furo com raio r deve ser feito no centro do bloco homogêneo. Determine a profundidade h do furo de modo que o centro de gravidade G seja o mais baixo possível.
Determine a profundidade h do furo de 100m m de diâmetro feito na base do cone de modo que o centro de massa do sólido resultante esteja localizado em z -=115m m . O material tem densidade de 8M g / m