Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 93
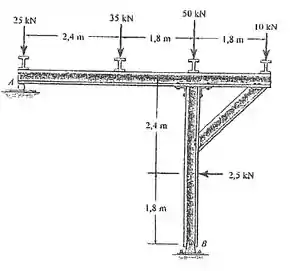
Determine as reações nos apoios e da estrutura.
Passo 1
Falaaa, querido! A gente quer as reações em e . Em , temos um pino, aí as reações estão nas duas direções. Já em só temos uma reação vertical. Vamos para o nosso DCL:
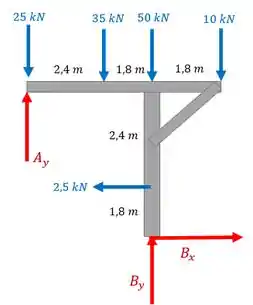
Como estamos no equilíbrio, a gente pode usar as equações de equilíbrio de forças e momento.
Passo 2
A força de reação em pode ser obtida diretamente através da soma dos momentos em relação ao ponto . Porque quando analisamos o momento em , as reações nesse ponto não aparecem na equação.
Então, galera, a primeira coisa que vamos analisar é a soma dos momentos em relação a !
Vamos assumir que o momento no sentido anti-horário é positivo:
Isolando :
Passo 3
Para a gente encontrar as componentes horizontal e vertical no ponto , vamos analisar cada um dos eixos separadamente. Vamos olhar primeiro para a componente horizontal.
A soma das componentes horizontais em deve ser igual a zero na situação de equilíbrio e vamos assumir como referência a direção para direita como positiva. Assim:
Passo 4
Vamos agora para a componente vertical. A soma das componentes verticais deve ser igual a zero na situação de equilíbrio e vamos assumir como referência a direção para cima como positiva. Assim: