Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 127

Localize o centroide overset(-)(y) da área sombreada.

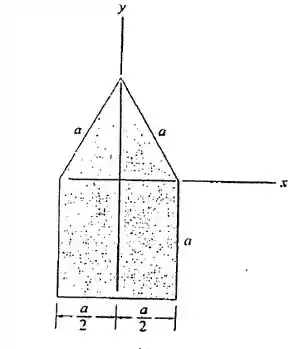
Passo 1

O problema pede que encontremos o centroide no eixo overset(-)(y) , para isso vamos usar a formula do centroide para figuras compostas

overset(-)(y) = (sum overset(-)(y) A)/(sum A)

Vamos separar nossa figura em duas regiões, um triângulo(1) e o retângulo(2):]

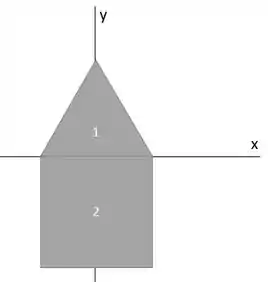
Aí a gente acha a área de cada uma, e também acha a coordenada y do centroide de cada uma em relação a esse sistema de coordenadas que a gente tem.

Passo 2

Para calcular o que a gente precisa, precisamos da altura do triângulo. Podemos achar fazendo pitagoras, porque uma das metades dele é um triângulo retângulo

a^2 = h^2 + ((a)/(2))^2

h = sqrt(a^2 - ((a)/(2))^2)

Aí nossas áreas ficam

A_1 = (h a)/(2) = (a)/(2) sqrt(a^2 - ((a)/(2))^2)

A_2 = a^2

Passo 3

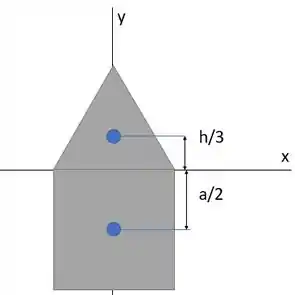
O centroide do triângulo fica a um terço da base. Como nossa origem de y está na base

overset(-)(y_1) = (h)/(3) = (1)/(3) sqrt(a^2 - ((a)/(2))^2)

E do retângulo, o centroide fica no seu centro. Como ele está na parte negativa de y , colocamos um sinal de menos

overset(-)(y_2) = - (a)/(2)

Podemos colocar essas coisas numa tabelinha e já calcular os somatórios:

Passo 4

Então agora usar a formula do primeiro passo, com as informações do passo anterior para calcular o centroide:

overset(-)(y) = (sum overset(-)(y) A)/(sum A) = (- (8 a^3)/(24))/(a^2 * (1 + (sqrt(3))/(4))) = - (8 a)/(24 * (1 + (sqrt(3))/(4)))

overset(-)(y) = - 0,263 a

Resposta

overset(-)(y) = - 0,263 a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A placa composta é feita de segmentos de aço ( A ) e latão ( B ) . Determine a massa e a localização ( x - ,y - ,z - ) de seu centro de massa G . Considere ρ a ç o = 7,85M g / m 3 ç e ρ l a t ã o = 8,
Determine a distância z - até o centroide do sólido que consiste em um cone com um furo de altura h=50m m feito em sua base.
Determine a localização y do centroide C da viga com a seção transversal mostrada.
Localize o centroide y da seção transversal da viga montada a partir de uma canaleta e de uma placa. Suponha que todos os cantos sejam “vivos” e desconsidere o tamanho da solda em A.
Determine a localização y do eixo x–x que passa pelo centroide da área transversal da viga. Para o cálculo, desconsidere o tamanho das soldas nos cantos em A e B.