Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 119
Determine o momento de inércia de área em relação ao eixo . Depois usando o teorema dos eixos paralelos, determine o momento de inércia em relação ao eixo que passa pelo centroide da área.
Passo 1
O problema pede que encontremos o momento de inércia no eixo e no eixo paralelo .
O problema nos dá que:
Agora, de forma diferencial pela área da curva:
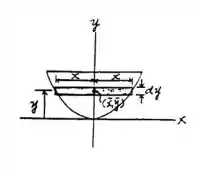
Passo 2
Então, vamos para o momento de inércia em relação ao eixo , que é dado pela integral:
Resolvendo a integral, temos:
Passo 3
E por fim, para encontrar o momento de inércia em relação ao eixo , nós usamos o teorema de dos eixos paralelos, que é:
Onde, a área é encontrada pela integral da equação do passo 1.
Com o resultado da integral, obtemos:
Então, substituindo no teorema, ficamos com:
Assim encontramos: