Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 87
Resolva o Problema 10.81 usando o círculo de Mohr.
Passo 1
O problema pede que encontremos a orientação dos eixos principais, os momentos e produtos de inércia, usando para isso o círculo de Mohr, que você pode encontrar uma explicação aqui mesmo no responde aí, dá uma olhadinha lá!
Então, vamos calcular o momento e o produto de inércia com relação aos eixos e :
Vamos para o eixo agora:
E também , que é:
Passo 2
Agora, iremos usar o círculo de Mohr, onde o centro do círculo encontra o eixo , então, vamos lá:
Passo 3
Calculamos então as cordenadas de referência do ponto são:
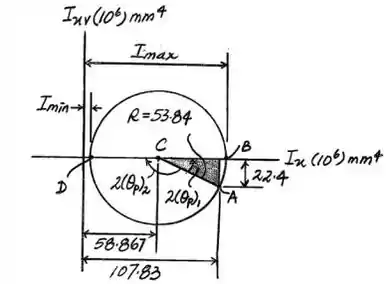
Logo, o circulo pode ser construído assim:
Passo 4
Com todas essas informações que obtemos, podemos calcular os momentos de inércia que são:
Então, também temos que saber que a orientação em relação aos eixos são:
Anti-horário
E:
Horário
Dessa forma:
