Determine o coeficiente de atrito estático mínimo entre a bobina uniforme de 50k g e a parece de modo que bobina não deslize.

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 14

Determine o coeficiente de atrito estático mínimo entre a bobina uniforme de e a parece de modo que bobina não deslize.

Passo 1

Fala ai galerinha bonita, tudo beleza?

Saca só, esse problema pede pra gente encontrar o menor coeficiente de atrito estático para que a bobina não deslize.

Vamos fazendo um diagrama de corpo livre, desse jeito:

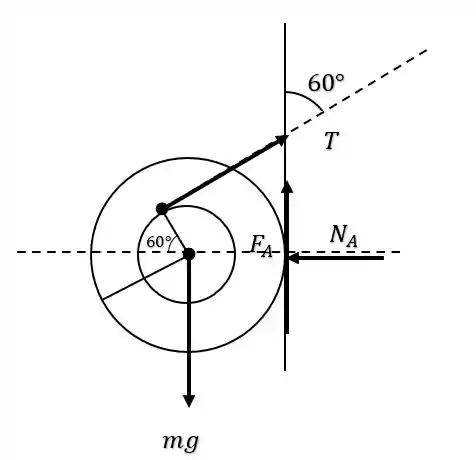
A gente nota, que faz uma força que causa um momento no sentido anti-horario no centro de massa, e isso equilibra o momento de rotação causado pela força , então a força é:

Passo 2

Agora, vamos aplicar a equação de equilíbrio no momento de :

Logo:

Passo 3

Por fim, vamos pegar a equação de equilíbrio para as forças:

O mesmo que:

E no eixo agora:

Então se a gente isolar

Dessa forma, a gente encontra:

Ou seja intependente da massa o coeficiente de atrito deve ser de no mínimo .

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

6/33) Assumindo que o trabalhador seja forte o suficiente , será possível manter o equilíbrio da prancha uniforme de 7m na posição mostrada , exercendo uma força horizontal na corda ? O coeficiente de

6/29) Repita o Prob.6/27 , mas agora o carro tem tração nas quatro rodas . Assuma que o deslizamento ocorre simultaneamente em A e B .

6/28) Repita o Prob.6/27 , mas agora o carro tem tração dianteira .

6/30) A barra uniforme com centro de massa em G é suportada pelas cavilhas A e B que estão presas à roda . Se o coeficiente de atrito entre a barra e as cavilhas é μ , determine o ângulo θ que a roda

6/26) Calcule a força T necessária para girar o carretel de cabo telefônico de 200k g , que se apoia em seu eixo e está enconstado contra uma parede vertical. O coeficiente de atrito dinâmico para cad