Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 10.Problemas - Ex. 40
10.55 Determine o momento de inércia da área da seção transversal em relação ao eixo .
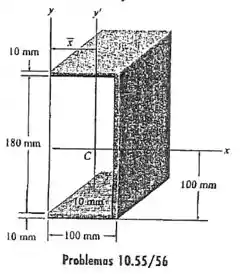
Passo 1
Vamos dividir essa área em 2 retângulos:
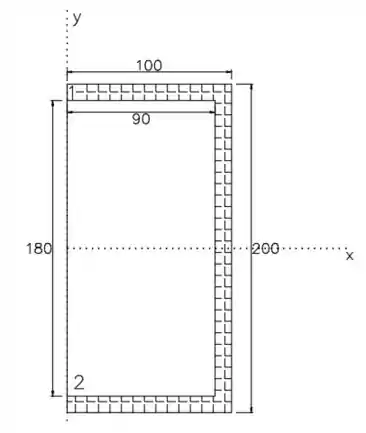
O momento de inercia total, será o momento de inercia do retângulo menos o momento de inercia do retângulo
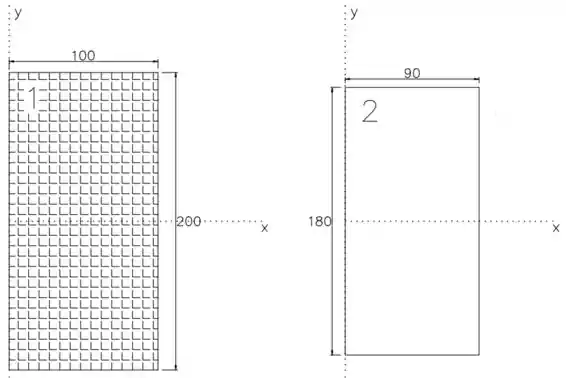
O momento de inercia de um retângulo, em relação ao eixo , é igual a . E como o centroide dos dois retângulos passam pelo eixo , não será necessário usar o teorema dos eixos paralelos.