Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas de Revisão - Ex. 2

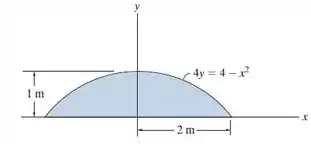
Determine o momento de inércia da área sombreada em relação ao eixo x .

Passo 1

E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!

Esta é uma questão bem direta! Precisamos calcular o momento de inércia da área em relação ao eixo y . Por definição, este momento é dado por:

I x = ∫ A y 2 d A

Então, basta resolvermos esta integral!

Temos aqui uma região do tipo I, cujos limites de integração são - 2 ≤ x ≤ 2 e 0 ≤ y ≤ 1 - x 2 4 .

Fazendo esta substituição, chegamos a seguinte integral:

I x = ∫ - 2 2 ∫ 0 1 - x 2 4 y 2 d y d x

Então, vamos as contas!

Passo 2

Agora nosso trabalho é braçal. Precisamos desenvolver a integral do Passo 1. Portanto,

I x = ∫ - 2 2 ∫ 0 1 - x 2 4 y 2 d y d x

I x = ∫ - 2 2 y 3 3 0 1 - x 2 4 d x

I x = ∫ - 2 2 1 - x 2 4 3 3 d x

I x = 1 3 ∫ - 2 2 1 - x 2 2 + x 4 16 1 - x 2 4 d x

I x = 1 3 ∫ - 2 2 1 - 3 x 2 4 + 3 x 4 16 - x 6 64 d x

I x = 1 3 x - x 3 4 + 3 x 5 80 - x 7 448 - 2 2

I x = 1 3 4 - 4 + 2,4 - 0,571

I x = 0,610   m 4

E assim finalizamos a questão!

Resposta

I x = 0,610   m 4

Ver Outros Exercícios desse livro