Enunciado
Física - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas - Ex. 64
Determine a intensidade e o sentido direcional da força em em relação ao ponto .
Passo 1
Oi, tudo bem? Vamos resolver esta questão que se parece muito com a anterior.
Queremos a intensidade e o sentido direcional da força em , agora, em relação ao ponto .
Observe o diagrama abaixo:
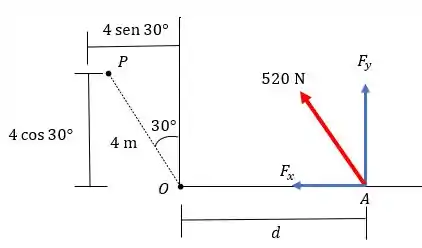
Analisando o diagrama, é possível observar que as componentes e irão agir no ponto . Portanto, fazendo o somatório de momento em . Temos que:
Resolvendo, temos que:
A força em causa um momento de no sentido anti-horário no ponto .
Resposta
Exercícios de Livros Relacionados
Você deseja localizar o centro de gravidade de um objeto achatado e de formato arbitrário. Você pendura o objeto de um ponto e um fio de prumo do mesmo ponto. Então, você traça uma linha vertical no o
Use o teorema dos eixos paralelos e o resultado do problema 41 para encontrar o momento de inércia do sistema de quatro partículas da figura 9-45 em relação a um eixo que passa pelo centro de massa e
Um cilindro oco tem massa m , raio externo R 2 e raio interno R 1 . Use integração para mostrar que o momento de inércia em relação a seu eixo é dado por I = 1 2 m ( R 2 2 + R 1 2 ) . Dica: reveja a s
Um disco uniforme de raio r e massa M gira em torno de um eixo horizontal paralelo ao seu eixo de simetria e que passa por um ponto de seu perímetro, de forma a poder oscilar livremente em um plano ve
Você pendura um aro fino de raio R em um prego na periferia do aro. Você o desloca lateralmente (dentro do plano do aro) até um ângulo β a partir de sua posição de equilíbrio e a seguir o liberta. Qua