Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 2

Determine o momento de inércia de um cone em relação a um eixo vertical y - que passa pelo centro de massa do cone. Qual é o momento de inércia em relação a um eixo paralelo y ' que passa pelo diâmetro da base do cone? O cone tem uma massa m.

Passo 1

Nota-se que a massa infinitesimal do cone d m , é tal que pode ser escrita como:

d m = ρ d V = ρ ( π y 2 ) d x = ρ π a 2 h 2 x 2 d x

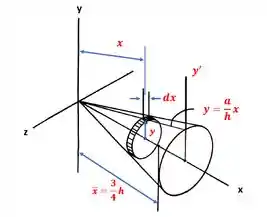
Passo 2

O momento de inércia para o elemento diferencial d I v será:

d I y = 1 4 d m y 2 + d m x 2

d I y = 1 4 ρ π a 2 h 2 x 2 d x a h x 2 + ρ π a 2 h 2 x 2 d x x 2

d I y = ρ π a 2 4 h 4 4 h 2 + a 2 x 4 d x

O momento de inércia I y é obtido integrando-se   d I y , de modo que:

I y = ∫ d I y = ρ π a 2 4 h 4 4 h 2 + a 2 ∫ 0 h x 4 d x = ρ π a 2 h 20 4 h 2 + a 2

Passo 3

A massa m , será:

m = ∫ d m = ρ π a 2 h 2 ∫ 0 h x 2 d x = ρ π a 2 h 3

Logo:

I y = 3 m 20 4 h 2 + a 2

Passo 4

Utilizando o teorema de eixos paralelos é possível obter o momentos em y - e y ' respectivamente. Logo:

I y = I y - + m d 2

3 m 20 4 h 2 + a 2 = I y - + ρ π a 2 h 3 3 h 4 2

I y - = 3 m 80 h 2 + 4 a 2

I y - = I y ' + m d 2

3 m 80 h 2 + 4 a 2 = I y ' + ρ π a 2 h 3 h 4 2

I y ' = m 20 2 h 2 + 3 a 2

Resposta

De acordo com os passos 1,2,3 e 4 , os momentos de inércia nos eixos verticais paralelos y - e y ' em um cone, serão respectivamente :

I y - = 3 m 80 h 2 + 4 a 2

I y ' = m 20 2 h 2 + 3 a 2

y = a h x

Ver Outros Exercícios desse livro