Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 155

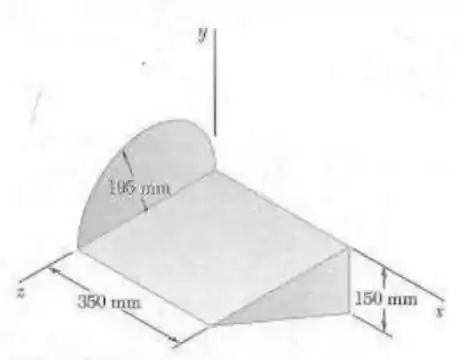
Uma seção de chapa de aço de 2 m m   de espessura é cortada e dobrada para formar o componente de máquina mostrado na figura. Sabendo que a massa específica do aço é 7850 k g / m 3 , determine os produtos de inércia I x y , I y z   e   I z x do componente.

Passo 1

Vamos dividir nossa seção de chapa em três partes: um semi- círculo de raio 0.195 m , um retângulo e um triângulo. Porém, vamos calcular primeiramente a massa de cada uma dessas partes que serão dadas pro

m 1 = 7850 ⋅ 0.002 ⋅ 0.35 ⋅ 0.39 = 2.14305 k g

m 2 = 7850 ⋅ 0.002 ⋅ π 2 ⋅ 0.195 2 ≈ 0.93775   k g

m 3 = 7850 ⋅ 0.002 ⋅ 1 2 ⋅ 0.39 ⋅ 0.15 = 0.45923   k g

Pela simetria do problema o produto inercial do retângulo e do semi-círculo serão iguais a 0 . Além disso, também temos

I x ' y ' - 3 = I z ' x ' - 3 = 0  

  I y ' z ' - 3 = ρ a ç o ⋅ t ⋅ I y ' z ' - 3 , a r e a = ρ a ç o ⋅ t ⋅ 1 72 ⋅ b 3 2 ⋅ h 3 2 = 1 36 ⋅ m 3 ⋅ b 3 ⋅ h 3

E ainda

y 1 - = x 2 - = 0   ,     y 2 - = 4 ⋅ 0.195 3 π ≈ 0.082761 m

Passo 2

Finalmente, teremos

I x y = ∑ I x ' y ' - + m x - y - = 0 + 0.45923 ⋅ 0.35 ⋅ - 0.15 3 → I x y = - 8.04 ⋅ 10 - 3   k g ⋅ m 2

I y z = ∑ I y ' z ' - + m z - y -

→ 0.93775 ⋅ 0.082761 ⋅ 0.195 + 1 36 ⋅ 0.45923 ⋅ 0.39 ⋅ 0.15 + 0.45923 ⋅ - 0.15 3 ⋅ 0.39 3 ≈ 12.895 ⋅ 10 - 3   k g ⋅ m 2

I z x = ∑ I x ' z ' - + m z - x - → 2.14305 ⋅ 0.175 ⋅ 0.195 + 0.459923 ⋅ 0.39 3 ⋅ 0.35

→ I z x ≈ 94 ⋅ 0266 ⋅ 10 - 3 k g ⋅ m 2

Resposta

I x y = - 8.04 ⋅ 10 - 3   k g ⋅ m 2

I y z = 12.9 ⋅ 10 - 3   k g ⋅ m 2

I z x = 94 ⋅ 10 - 3 k g ⋅ m 2

Ver Outros Exercícios desse livro