Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 143

Determine o momento de inercia de massa do elemento de maquina de aço mostrado n a figura em relação ao eixo z . (O peso especifico do aço é especifico do aço é 490   l b / f t 3 ) .

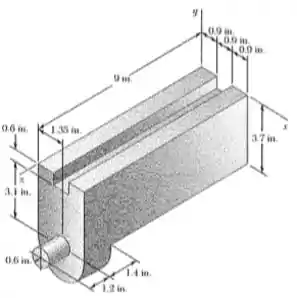
Passo 1

Igual a questão passada, o que muda é somente o eixo, então vamos repetir o primeiro passo ! Primeiro, vamos pegar o numero de massa de cada elemento! Vamos considerar como elemento 1 o paralelepípedo grande (sem considerar o semilidindro e o cilindro de baixo), elemento 2 o semi cilindro de baixo, elemento 3 o cilindro e elemento 4 a fenda que fica em cima da peça.

m = ρ V

Podemos também considerar a nossa equação a partir do peso específico. Que é:

m = γ g V

m 1 = 490 32.2 × 2.7 × 3.7 × 9 × 1 12 3 = 791.78 × 10 - 3 l b ⋅ s 2 / f t

m 2 = 490 32.2 × π 2 × 1.35 2 × 1.4 × 1 12 3 = 35.298 × 10 - 3 l b ⋅ s 2 / f t

m 3 = 490 32.2 × π × 0.6 2 × 1.2 × 1 12 3 = 11.952 × 10 - 3 l b ⋅ s 2 / f t

m 4 = 490 32.2 × 0.9 × 0.6 × 9 × 1 12 3 = 42.799 × 10 - 3 l b ⋅ s 2 / f t

Passo 2

Agora que temos as massas, vamos aplicar o teorema dos eixos pararelos, para achar os momentos de inercia de massa de cada elemento e soma-los!

I y = I y 1 + I y 2 + I y 3 - I y 4

= 1 12 791.78 × 10 - 3 2.7 2 + 9 2 +   791.78 × 10 - 3 2.7 2 2 + 9 2 2 2 × 1 12

+ 1 12 35.298 × 10 - 3 1 2 - 16 9 π 2 +   35.298 × 10 - 3 1.35 2 + 3.7 - 4 × 1.35 3 π 2 × 1 12

+ 1 12 11.952 × 10 - 3 0.6 2 +   11.952 × 10 - 3 1.35 2 + ( 3.7 ) 2 × 1 12

- 1 12 42.799 × 10 - 3 0.9 2 + ( 0.6 ) 2 +   42.799 × 10 - 3 1.35 2 + 0.6 2 2 × 1 12

= 0 . 0442   l b ⋅ f t ⋅ s 2

Resposta

I z = 0.0442   l b ⋅ f t ⋅ s 2

Ver Outros Exercícios desse livro