Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 107

Determine o momento de inércia da massa da manivela em relação ao eixo x . O material é aço, com uma densidade de ρ = 7,85   M g / m 3 .

Passo 1

O problema pede que encontremos o momento de inércia no eixo x .

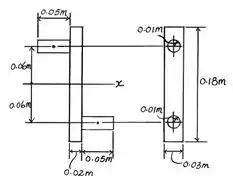
Primeiro, vamos pensar sobre as massas, m 1 :

m 1 = ρ ⋅ V 1 = ρ h π r 2

m 1 = 7,85 ⋅ 10 3 ( 0,05 ) π ( 0 , 01 2 ) = 0,1233   k g

Agora, m 2 :

m 2 = ρ ⋅ V 2 = ρ a h b

m 2 = 7,85 ⋅ 10 3 ( 0,03 ) ( 0,18 ) ( 0,02 ) = 0,8478   k g

Passo 2

Vamos então, descobrir as formulas dos momentos de inércia de das placas e das esferas, que podemos encontrar no final do livro, e são dados por:

I x 1 = 1 2 m 1 ( a 2 + b 2 ) 2

I x 2 = 1 12 m 2 ( a 2 + h 2 )

Passo 3

E finalmente calculando o momento de inercia com as informações que temos, em relação ao eixo z , fica:

I x = I x 1 + I x 2

Então:

I x = 2 1 2 0,1233 0,03 2 + 0,1233 0,06 2 + 1 12 0,8478 0,03 2 + 0,18 2

Calculando isso, chegamos á:

I x = 0,00325   k g ⋅ m 2

Resposta

I x = 0,00325   k g ⋅ m 2

Ver Outros Exercícios desse livro