Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 110
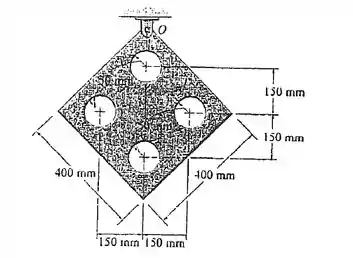
Determine o momento de inércia de massa da placa fina em relação a uma eixo perpendicular à página e que passa pelo ponto . O material tem uma massa por por unidade de área de .
Passo 1
Falaa!
O problema pede que encontremos o momento de inércia em relação a um eixo perpendicular à página e que passa pelo ponto .
Primeira coisa a reparar é que a figura é simétrica, então o centro de massa dela é no centro geométrico. Maas, o eixo não passa pelo centro de massa, então vamos achar o momento de inércia em relação ao centroide e depois vamos ter que usar o teorema dos eixos paralelos.
Segunda coisa: repara que temos uma figura composta. A gente tem esse quadrado inclinado que tem furinhos na forma de circulo. Então, a gente pode obter nossa placa que se pegar um quadrado e tirar as bolinhas, assim:
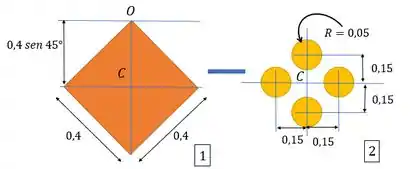
E o momento de inércia em relação ao centro de massa vai ser o momento da placa quadrada menos os momentos das bolinhas:
Como as bolinhas são iguais e estão posicionadas a mesma distância de , a gente vai achar o momento de uma e multiplicar por .
Uma coisa que vai ser útil para gente é ter as massas do quadrado e de um circulozinho desse. Vamos agora calcular as massas:
E:
Vamos seguir!
Passo 2
Então, vamos no final do livro pegar as fórmulinhas do momento de inércia em relação a . Para o quadrado, temos que
Onde e são os lados do quadrado.
Já para os círculos, percebe que o momento de inércia deles que vamos usar não deve ser em relação ao centro de massa de cada um separadamente, mas em relação a também. Por isso, a gente vai ter que usar aqui o teorema dos eixos paralelos também.
O momento de inércia de um círculo em relação ao seu centro de massa é
Onde é o raio do círculo. Mas vamos precisar usar o teorema dos eixos paralelos e escrever que
Onde é a distância entre o eixo que passa por (centro de massa do círculo) e (centro de massa da placa geral). Pela figura ela vale . Logo, podemos arrumar e chegar em
Agora, vamos calcular o momento de inercia com as informações que temos, em relação ao ponto , fica:
Então:
Calculando isso, chegamos á:
Passo 3
E finalmente vamos calcular o momento de inércia em relação ao ponto , para isso, usamos o teorema dos eixos paralelos:
Mas agora é a distância entre e , que pela figura, podemos calcular como
Sendo também que é massa total e é dada por:
Já que para formar nossa placa a gente tira os círculos do quadrado, então a massa dos círculos entra negativa.
Então calculando fica:
Cara, ficou um pouquinho diferente do gabarito, mas estamos certinhos!