Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 14
Determine as componentes horizontal e vertical da reação em e a tração no cabo sobre a lança ao problema .
Passo 1
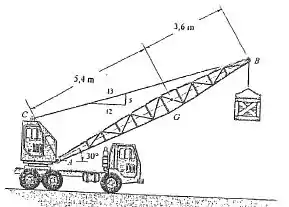
Falaaa, querido! A gente quer as reações em e a tração em . Repara que aqui a gente só quer analisar a lança. Vamos relembrar nosso DCL com os dados do problema:
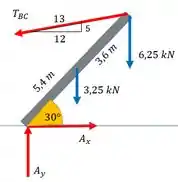
Ela tem o peso próprio de e suporta o peso de na ponta.
Na hora de decompor nos eixos coordenados, vamos usar as medidas do triângulo retângulo. Como está paralelo ao eixo vertical, a componente vertical dela vai ser e horizontal vai ser , porque está paralelo ao eixo horizontal.
Como estamos no equilíbrio, a gente pode usar as equações de equilíbrio de forças e momento.
Passo 2
A força no cabo pode ser obtida diretamente através da soma dos momentos em relação ao ponto . Porque quando analisamos o momento em , as reações nesse ponto não aparecem na equação.
Então, galera, a primeira coisa que vamos analisar é a soma dos momentos em relação a !
Vamos precisar decompor nos eixos coordenados e também as distâncias que temos porque elas estão inclinadas, para achar as forças e seu braços de alavanca direitinho.
Vamos assumir que o momento no sentido anti-horário é positivo:
Passo 3
Para a gente encontrar as componentes horizontal e vertical no ponto , vamos analisar cada um dos eixos separadamente. Vamos olhar primeiro para a componente horizontal.
A soma das componentes horizontais em deve ser igual a zero na situação de equilíbrio e vamos assumir como referência a direção para direita como positiva. Assim:
Passo 4
Vamos agora para a componente vertical. A soma das componentes verticais deve ser igual a zero na situação de equilíbrio e vamos assumir como referência a direção para cima como positiva. Assim:
Resposta
Os valores para as componentes de reação em são:
O valor da tensão no cabo é: