Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 19

Determine o momento de inércia da montagem barras e anel fino em relação ao eixo z . As barras e o anel têm uma massa por unidade de comprimento de 2   k g / m .

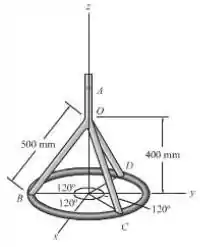
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Para o disco temos:

u x ' = 0,6

u y ' = 0

u z ' = 0,8

Temos que:

I x = I y = 1 3 0,5 2 0,5 2

I x = I y = 0,08333   k g ⋅ m 2

Sabemos que:

I x ' = 0

I x ' y ' = I y ' z ' = I x ' z ' = 0

Portanto:

I z = I x ' u x ' 2 + I y ' u y ' 2 + I z ' u z ' 2 - 2 I x ' y ' u x ' u y ' - 2 I y ' z ' u y ' u z ' - 2 I x ' z ' u x ' u z '

I z = 0,08333 0,6 2 + 0 + 0 - 0 - 0

I z = 0,03   k g ⋅ m 2

Para o anel, temos:

r = 0,3   m

Logo:

I z = m R 2 = 2 2 π 0,3 0,3 2

I z = 0,3393   k g ⋅ m 2

Portanto, o momento de inércia total, é dadp pela soma dos componentes:

I z = 3 0,03 + 0,3393

I z = 0,429   k g ⋅ m 2

Resposta

I z = 0,429   k g ⋅ m 2

Ver Outros Exercícios desse livro