Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 51
O disco de 25 kg gira com uma taxa angular constante em torno de seu eixo. Simultaneamente, o eixo gira com uma taxa angular constante . Determine as componentes x,y, z do momento desenvolvido no braço A no instante mostrado. Despreze o peso do braço AB.
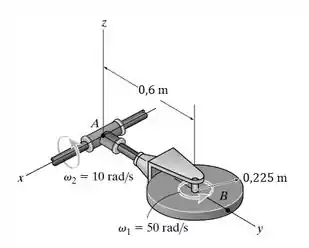
Passo 1
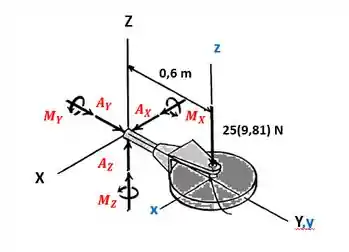
O sistema descrito acima terá velocidade angular :
Como o disco é simétrico em relação ao seu eixo de rotação, os eixos x, ye z permanecerão como os eixos principais da inércia. De forma que:
Passo 2
A velocidade angular do disco é , de modo que:
Como as direções de e não mudam em relação aos eixos xyz e suas magnitudes são constantes, .Assim,
Passo 3
De acordo com o diagrama de corpo livre descrito, pode-se inferir as seguintes equações de movimento:
(1)
Passo 4
A aceleração do centro de massa do disco será:
Assim :
Portanto, substituindo o valor de em (1), o momento em X será:
Resposta
De acordo com os passos 1,2,3 e 4 as componentes x,y, z do momento desenvolvido no braço A no instante mostrado serão respectivamente: