Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 20

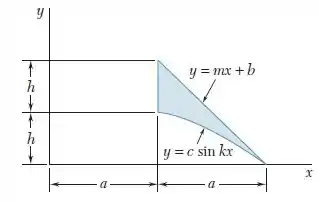
Determine o momento de inércia e o raio de rotação da área sombreada mostrada em relação ao eixo y .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O momento de inércia neste caso é dado por:

d I y = x 2 d A

Desta forma, temos que:

d I y = x 2 2 h a ( 2 a - x ) - h sen ⁡ π x 2 a d x

A integral do momento de inércia é dada por:

I y = ∫ a 2 a d I y

I y = ∫ a 2 a x 2 2 h a ( 2 a - x ) - h sen ⁡ π x 2 a d x

Resolvendo a integral com o auxílio computacional, temos que:

I y = h 2 a - 4 a 4 + 16 a 4 3 - 8 a 3 π + 16 a 3 π 3 - h 2 a - a 4 4 + 2 a 4 3 - 8 a 3 π 2

Passo 2

Simplificando, temos que:

I y = 0,6134 a 3 h

O raio de giração em relação ao eixo y é dado por:

k y 2 = I y A

Substituindo os valores, temos que:

k y 2 = 0,6134 a 3 h 0,3634 a h

Logo:

k y = 1,3 a

Resposta

I y = 0,6134 a 3 h

k y = 1,3 a

Ver Outros Exercícios desse livro