Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 18

Determine os momentos de inércia I x x ,   I y y ,   I z z para a barra dobrada. A barra tem uma massa por unidade de comprimento de 2   k g / m .

Passo 1

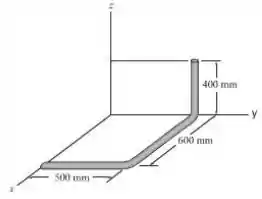
Oi pessoal, tudo bem? Vamos analisar essa questão.

Bom, a estratégia para resolver produtos de inércia é dividir o desenho de uma forma que nos ajude. E calcular os produtos de cada um separadamente.

Vamos calcular o produto de Inércia de cada barra aplicando no somatório.

Temos que:

I x x = ∑ ( T x ' x ' + m y G 2 + z G 2

I x x = 1 12 ( 0,4 ) ( 2 ) ( 0,4 2 ) + 0,4 2 0,5 2 + 0,2 2 + 0 + 0,6 ( 2 ) ( 0,5 2 + 0 2 ) + 1 12 ( 0 , 5 ) ( 2 ) ( 0 , 5 2 ) + 0 , 5 2 0 , 2 5 2 + 0 2

I x x = 0 , 626   k g ⋅ m 2

I y y = ∑ ( T y ' y ' + m x G 2 + z G 2

I y y = 1 12 ( 0,4 ) ( 2 ) ( 0,4 2 ) + 0,4 2 0 2 + 0,2 2 + 1 12 ( 0 , 6 ) ( 2 ) ( 0 , 6 2 ) + 0,6 ( 2 ) ( 0,3 2 + 0 2 ) + 0 + 0,5 2 0 , 6 2 + 0 2

I y y = 0 , 547   k g ⋅ m 2

I z z = ∑ ( T z ' z ' + m x G 2 + y G 2

I z z = 0 + 0,4 2 0 2 + 0,5 2 + 1 12 ( 0,6 ) ( 2 ) ( 0,6 2 ) + 0,6 ( 2 ) ( 0,3 2 + 0 , 5 2 ) + 1 12 ( 0 , 5 ) ( 2 ) ( 0 , 5 2 ) + 0,5 2 0,6 2 + 0 , 25 2

I z z = 1,09   k g ⋅ m 2

Resposta

I x x = 0,626   k g ⋅ m 2

I y y = 0,547   k g ⋅ m 2

I z z = 1,09   k g ⋅ m 2

Ver Outros Exercícios desse livro