Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 78
Determine os momentos de inércia e o produto de inércia da área da seção transversal da viga em relação aos eixos u e v.
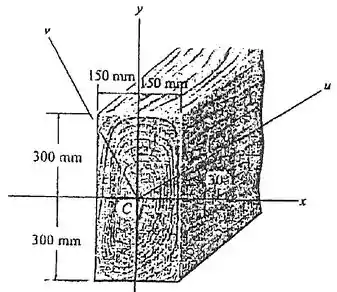
Passo 1
Fala, querido! Ele quer os momentos de inércia e o produto de inércia em relação a esses eixos inclinados. Mas a nossa figura é bem simples em relação a e .
Então o que a gente vai fazer é calcular os momentos e produto para e . E depois jogar nas fórmulinhas para achar esses valores para um rotação dos eixos que nos dê e .
Desenho:
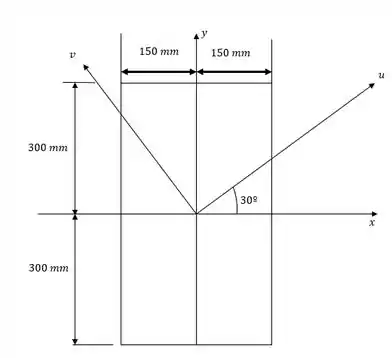
Passo 2
Vamos calcular inicialmente os momentos de inércia e . Como temos um seção retangular:
Percebe que a gente deixa sem o expoente quem é o comprimento do segmento do retângulo que é paralelo ao eixo em questão.
A seção transversão retangular é simétrica em relação ao eixo x, então
Passo 3
Calculando o produto de inércia em relação ao novo sistema de coordenadas, vamos usar a fórmulinha:
Para chegar no novo sistema de coordenadas, vamos girar um ângulo de no sentido anti-horário. Então vai ser um ângulo positivo. Aí substituindo na fórmulinha
A fórmulinha para um eixo perpendicular a (o nosso ) vai ser
Percebe que mudam alguns sinais, mais , porque ele é medido em relação a . Substituindo:
E para o produto de inércia nós usamos: