Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 50
O utilitário com tração nas quatro rodas de tem centro de massa em . Determine a massa máxima da tora que pode ser rebocada pelo automóvel. O coeficiente de atrito estático entre a tora e o solo é , e o coeficiente de atrito estático entre as rodas do carro e o solo é . As rodas traseiras são livres para rolar. Assuma que o moto do carro seja poderoso o bastante para gerar um torque que fará todas as rodas dianteiras deslizarem.
Passo 1
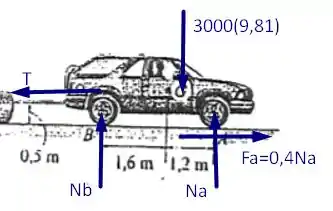
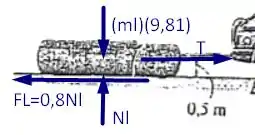
Desejamos encontrar o valor da massa máxima para a tora de tal forma que o carro possa rebocá-la, levando em consideração que agora as rodas traseiras são livres para rolar. Assim, tomemos os seguintes diagramas de forças para o carro e a tora respectivamente
Passo 2
Tomando as equações de equilíbrio para o nosso diagrama de forças do carro teremos
Passo 3
Agora, fazendo a mesma análise para o diagrama de forças da tora vamos ter o seguinte