Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 102

Se F 1 = 500   N e F 2 = 1000   N , determine a intensidade e os ângulos coordenados do momento de binário resultante.

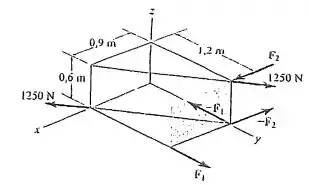
Passo 1

O problema pede a vetor momento de binário resultante de um sistema composto por três binários.

A fórmula para um binário de duas forças antiparalelas separadas por um vetor r → é

M → = r → × F →

Assim, temos que calcular cada um dos binários e somá-los vetorialmente. Neste problema, teremos:

r 1 → = a   i ^               e                 F 1 → = F 1   j ^

r 2 → = b   k ^               e                 F 2 → = F 2   i ^

r 3 → = b   k ^             e               F 3 → = F 3 a 2 + c 2   - a   i ^ + c   j ^

Onde temos que a = 0,9   m , b = 0,6   m , c = 1,2   m , F 1 = 500   N , F 2 = 1000   N e F 3 = 1250   N .

Passo 2

Calculando os produtos vetoriais:

M 1 → = a   i ^ × F 1   j ^ = a F 1   k ^

M 2 → = b   k ^ × F 2   i ^ = b F 2   j ^

M 3 → = b   k ^ × F 3 a 2 + c 2   - a   i ^ + c   j ^ = - b F 3 a 2 + c 2 c   i ^ + a   j ^

Portanto,

M → = M 1 → + M 2 → + M 3 → = - b c   F 3 a 2 + c 2   i ^ + - b a   F 3 a 2 + c 2 + b F 2   j ^ + a F 1   k ^

Passo 3

Substituindo a = 0,9   m , b = 0,6   m , c = 1,2   m , F 1 = 500   N , F 2 = 1000   N e F 3 = 1250   N , encontramos:

M → = - 600   i ^ + 15 0   j ^ + 450   k ^   N ⋅ m

A intensidade do momento resultante será

M = 600 2 + 150 2 + 450 2 = 764,8   N ⋅ m

Resposta

M → = - 600   i ^ + 150   j ^ + 450   k ^   N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Substitua as três forças atuando na chapa por um torsor. Especifique a intensidade da força e o momento de binário para o torsor e o ponto P ( x , y ) onde sua linha de ação intercepta a chapa.
Se F a = 40 k N e F b = 35 k N , determine a intensidade da força resultante e especifique a posição de seu ponto de aplicação ( x , y ) sobre a placa.
Substitua as três forças que agem na chapa por um torsor. Especifique a intensidade da força e o momento de binário para o torsor e o ponto P ( x , y ) , onde sua linha de ação intercepta a chapa.
Se a força resultante deve agir no centro da placa, determine a intensidade das cargas das colunas F aeF b e a intensidade da força resultante.
Se a força em cada corrente possui uma intensidade de 2,25 k N , determine a intensidade e os ângulos de direção coordenados da força resultante.