Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 41

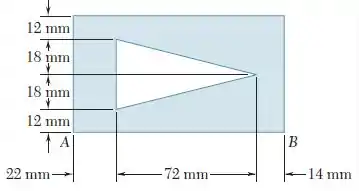
Determine os momentos de inércia I x e I y da superfície mostrada na figura em relação aos eixos centroidais paralelo e perpendicular ao lado A B , respectivamente.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

A estrutura foi dividida conforme a figura a seguir:

A área do retângulo 1 é dada por:

A 1 = b 1 h 1

A 1 = 108 60

A 1 = 6480   m m 2

A área do triângulo 2 é dada por:

A 2 = b 2 h 2 2

A 2 = 1 2 36 72

A 2 = 1296   m m 2

Logo, a área sombrea da é dada por:

A = A 1 - A 2

A = 5184   m m 2

Passo 2

Agora, vamos calcular o centroide ao longo do eixo x usando a fórmula:

X - ∑ A = ∑ x - A

X - 5184 = 54 6480 - 22 + 72 3 1296

X - 5184 = 290304

X - = 290304 5184

Logo:

X - = 56   m m

Da simetria da figura, podemos inferir que:

Y - = 18 + 12

Y - = 30   m m

Passo 3

Agora que temos o centroide podemos calcular o momento de inércia. Vamos calcular o momento em relação ao eixo x sobre cada área:

I x 1 = 1 12 b 1 h 1 3

I x 1 = 1 12 108 60 3

I x 1 = 1,944 ⋅ 10 6   m m 4

Para a área 2 , temos que:

I x 2 = 2 1 36 72 18 3 + 1 2 72 18 6 2

I x 2 = 69984   m m 4

Passo 4

O momento de inércia total sobre o eixo x é dado por:

I x = I x 1 - I x 2

I x = 1,944 ⋅ 10 6 - 69984

I x = 1,874 ⋅ 10 6   m m 4

Passo 5

Agora que temos o centroide podemos calcular o momento de inércia. Vamos calcular o momento em relação ao eixo y sobre cada área:

I y 1 = 1 12 108 3 60 + 108 60 56 - 54 2

I y 1 = 6,324 ⋅ 10 6   m m 4

Para a área 2 , temos que:

I y 2 = 1 36 72 3 36 + 1 2 72 36 56 - 22 + 72 3 2

I y 2 = 0,503 ⋅ 10 6   m m 4

Passo 6

O momento de inércia total sobre o eixo y é dado por:

I y = I y 1 - I y 2

I y = 6,324 ⋅ 10 6 - 0,503 ⋅ 10 6

I y = 5,821 ⋅ 10 6   m m 4

Resposta

I x = 1,874 ⋅ 10 6   m m 4

I y = 5,821 ⋅ 10 6   m m 4

Ver Outros Exercícios desse livro