Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 143

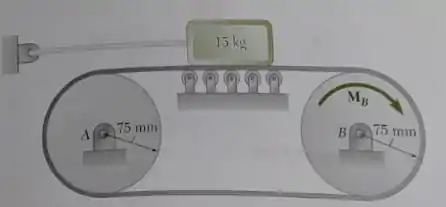
O binário M B é aplicado no giro do tambor motriz para manter a velocidade constante da cinta de polimento mostrada na figura. Sabendo que μ k = 0,45 entre a cinta e o bloco de 15   k g , inicia o polimento e μ s = 0,30 entre a cinta e o tambor motriz B , determine a o binário M B , b a mínima tração entre a parte inferior da cinta se nenhum escorregamento ocorre entre a cinta e o tambor motriz.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Determinando as reações do mecanismo, temos:

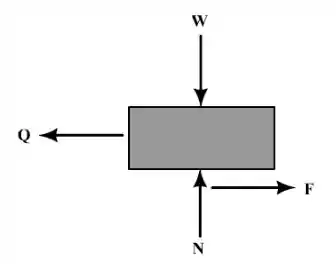
A partir da análise vertical, temos que:

∑ F y = N - W = 0

N = 147,15   N

A força de atrito:

F = μ k N

F = 66,2175   N

Passo 2

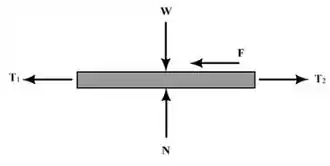
Analisando agora o diagrama da correia sob o bloco:

∑ F x = T 2 - T 1 - F

T 2 - T 1 = 66,2175   N

Passo 3

Agora vamos analisar o tambor B :

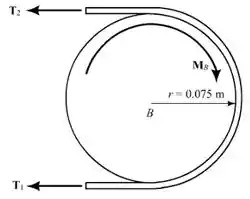
Para essa análise, temos que:

T 2 T 1 = e μ s β

T 2 T 1 = e 0,3 π

Resolvendo, temos que:

T 2 T 1 = 2,566

Logo:

T 2 = 2,566 T 1

Substituindo na equação do passo anterior, temos:

2,566 T 1 - T 1 = 66,2175   N

1,566 T 1 = 66,2175

T 1 = 42,277   N

Substituindo T 1 para encontrar T 2 , temos:

T 2 = 2,566 42,277  

T 2 = 108,484   N

Passo 4

Fazendo o momento sobre o ponto B , temos:

∑ M B = T 2 0,075 - M B - T 1 0,075 = 0

M B = 8,1363 - 3,170775

M B = 4,97   N ⋅ m

Resposta

a )   M B = 4,97   N ⋅ m

b )   T m í n = 42,277   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A caixa uniforme C de 60 kg se apoia uniformemente sobre uma plataforma móvel D de 10 kg. Se as  rodas  dianteiras  da  plataforma  em A  estão  travadas  para impedir o rolamento enquanto as rodas em
Determine a força máxima P que a conexão pode suportar de modo que não haja deslizamento entre as placas. Há quatro parafusos usados para a conexão e cada um é apertado de modo que esteja sujeito a um
O vagão de mina e seu conteúdo possuem massa total de 6 Mg e centro de gravidade em G . Se o coeficiente de atrito estático entre as rodas e os trilhos é μ s = 0,4 quando as rodas estão travadas, dete
A bobina com massa de 150k g se apoia sobre o piso em A e contra a parede em B. Determine as forças que agem na bobina em A e B se P=800N . O coeficiente de atrito estático entre a bobina e o piso no
O freio manual consiste em uma alavanca conectada por um pino e um bloco de atrito em B. O coeficiente de atrito estático entre a roda e a alavanca é u=0,3 , e um torque de 5Nm é aplicado à roda. Dete