Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 142
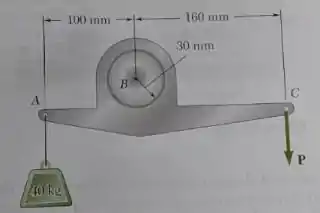
Uma alavanca de peso desprezível é montada com folga em um eixo de de raio mostrado na figura. Sabendo que a aplicação da força de intensidade irá justamente iniciar a rotação no sentido horário, determine o coeficiente de atrito estático entre o eixo e a alavanca. a menor força para que a alavanca não inicie a rotação no sentido anti-horário.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Acharemos o peso, que tem uma massa de . Assim poderemos analisar o momento de equilíbrio no ponto :
O momento em com sentido anti-horário positivo:
Substituindo os valores, temos que:
Passo 2
Item b:
Agora determinarems a menor força para que a alavanca não inicie a rotação no sentido anti-horário:
O momento em com sentido anti-horário positivo:
Resposta
Exercícios de Livros Relacionados
Os blocos A, B e C possuem pesos de 50N , 25N e 15N , respectivamente. Determine a menor força horizontal P que causará iminência de movimento. O coeficiente de atrito estático entre A e B é u s=0,3 ,
O came está sujeito a um momento de binário de 5N m . Determine a força mínima P que deverá ser aplicada ao seguidor para manter o came na posição mostrada. O coeficiente de atrito estático entre o ca
A escada uniforme de 10 kg se apoia no piso áspero para o qual o coeficiente de atrito estático é u s= 0,4 e contra a parede lisa em B. Determine a força horizontal P que o homem precisa exer
A viga uniforme de 25k g é suportada pela corda que está presa à sua extremidade, contorna o pino áspero e depois conecta-se ao bloco de 50k g . Se o coeficiente de atrito estático entre a viga e o bl
Um disco de 35k g se apoia sobre uma superfície inclinada para a qual u s=0,2 . Determine a força vertical P máxima que pode ser aplicada à viga AB sem fazer com que o disco deslize em C. Desconsidere