Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 81

Determine a orientação dos eixos principais, que têm sua origem no centroide C da área da seção transversal da viga. Além disso, determine os momentos principais de inércia.

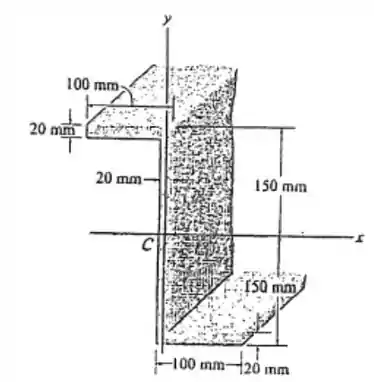
Passo 1

Desenho:

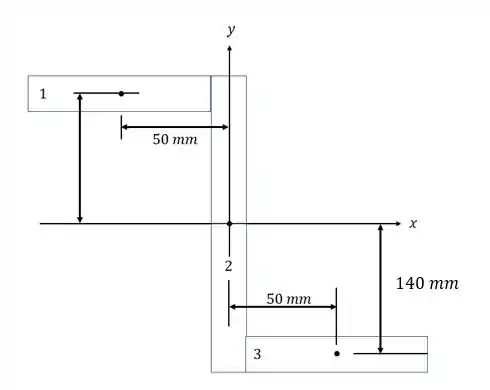
Passo 2

Organizando os momentos de inércia em relação ao eixo x em uma tabela:

Passo 3

Podemos calcular o momento de inércia em relação ao eixo x como:

I x = I x - + A d 2 I x = 45 , 106 × 10 6 + 62 , 6 2 × 10 6 I x = 107 , 7 × 10 6   m m 4

Passo 4

Organizando os momentos de inércia em relação ao eixo y em uma tabela:

Passo 5

Podemos calcular o momento de inércia em relação ao eixo y como:

I y = I y - + A d 2 I y = 1906,67 × 10 3 + 8 × 10 6 I y = 9,907 × 10 6   m m 4

Passo 6

Vamos para os produtos de inércia!

Devido à simetria, todas partes tem I x y = 0

Portanto o produto de inércia pode ser calculado como:

I x y = ∑ A d x d y I x y = 80 × 20 × - 50 × 140 ) + 300 × 20 × 0 × 0 + 80 × 20 × 50 × ( - 140 ) I x y = - 11,2 × 10 6 + 0 - 11,2 × 10 6 I x y = - 22,4 × 10 6   m m 4

Passo 7

Após calculados os momentos de inércia e o produto de inércia, os momentos principais de inércia I m á x   e   I m í n   podem ser calculados: I m á x / m i n = I x ±   I y 2 ± I x - I y 2 2 + I x y 2

I m á x / m i n = 107 , 7 +   9,907 2 ± 107 , 7 - 9,907 2 2 + - 22,4 2 × 10 6

I m í n = 5,02 × 10 6   m m 4 I m á x = 112 , 5 8 × 10 6   m m 4

tan ⁡ 2 θ p = - I x y ( I x - I y ) 2 tan ⁡ 2 θ p = - - 22,4 × 10 6 107 , 7 - 9,907 × 10 6 2 = 0,45 8 2 θ p = 24 , 61 º     e - 155 , 39 º θ p = 12,30 º   e - 77 , 69 º  

Resposta

I m í n = 5,02 × 10 6   m m 4 I m á x = 112,58 × 10 6   m m 4

θ p = 12,30 º   e - 77 , 69 º

Ver Outros Exercícios desse livro