Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 24
O tambor tem um peso de e repousa sobre o piso para o qual o coeficiente de atrito estático é . Se e , determinea menor intensidade da força que causará a iminência de movimento do tambor.
Passo 1
O problema pede que encontremos a força minima para que o o tambor fique á ponto de se mover.
Beleza, vamos começar fazendo um diagrama de corpo livre no tambor e analisando o momento do tambor, porque a gente sabe que ele tá na iminência de movimento, ou seja, ele tá em equilíbrio, logo:
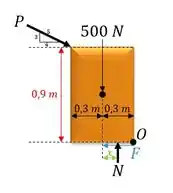
Passo 2
Então a gente resolve essa equaçãozinha e descobre :
A gente só conseguiu isso usando o momento, mas a gente também pode usar o somatório das forças e chegaremos também a:
Resposta
Exercícios de Livros Relacionados
Uma alavanca A B de peso desprezível é montada com folga em um eixo fixo de 63m m de diâmetro. Sabendo que o coeficiente de atrito estático entre o eixo fixo e a alavanca é 0,15 , determine a força P
Uma alavanca A B de peso desprezível é montada com folga em um eixo fixo de 63m m de diâmetro. Sabendo que o coeficiente de atrito estático entre o eixo fixo e a alavanca é 0,15 , determine a força P
Um vagão ferroviário tem massa 30M g e é apoiado em oito rodas de 800m m de diâmetro, com eixos de 125m m de diâmetro. Sabendo que os coeficientes de atrito são μ s = 0,020 e μ k = 0,015 , determine a
Resolva o Problema 8.10 8 supondo que a correia plana e os tambores sejam substituídos por uma correia em V e por polias em V com α = 36 ° . (O ângulo α é mostrado na Fig. 8.15 a .)
Resolva o Problema 8.126 considerando que θ = 75 ° .