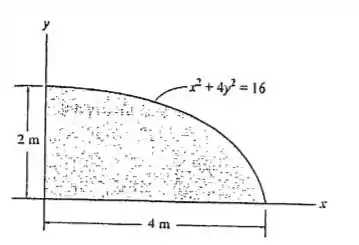
Determine o produto de inércia para a área da elipse em relação aos eixos e .

Fala ai galerinha do RespondeAí, tudo beleza??

Saca só, nesse exercício aqui, o enunciado quer que a gente encontre o produto de inércia para área da elipse em relação ao eixo e , no primeiro quadrante.

Iradoso, pra isso podemos lembrar que o produto de inércia nos eixos é dado como:

Sendo assim, teremos que para a elipse no primeiro quadrante, as coordenadas e serão: